搜索
【题目】如图所示，在□ABCD中，点E，F分别在边BC和AD上，且CE＝AF，
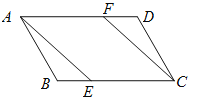
（1）求证：△ABE ≌ △CDF；
（2）求证：四边形AECF是平行四边形．
参考答案：
【答案】（1）证明见解析（2）证明见解析
【解析】试题分析：（1）由点E、F分别是ABCD的边BC、AD上的点，且CE=AF，可得AB=CD，∠B=∠D，BE=CF，则可由SAS证得：△ABE≌△CDF．
（2）由（1）得：AE=CF又CE＝AF，故四边形AECF是平行四边形．
试题解析：∵四边形ABCD是平行四边形，
∴AB=CD，AD=BC，∠B=∠D，
∵CE=AF，
∴AD-AF=BC-CE，
即BE=DF，
在△ABE和△CDF中，
，
∴△ABE≌△CDF（SAS）
（2）由（1）得：AE=CF
又CE＝AF
∴四边形AECF是平行四边形．
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知a、b、c在数轴上的位置如图所示，回答下列问题：
（1）化简：3|a﹣c|﹣2|﹣a﹣b|；
（2）令y＝|x﹣a|+|x﹣b|+|x﹣c|，x满足什么条件时，y有最小值，求最小值
-
科目： 来源： 题型：
查看答案和解析>>【题目】《函数的图象与性质》拓展学习片段展示：
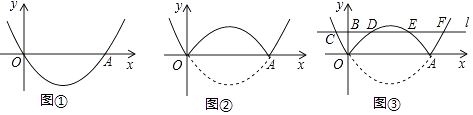
（1）【问题】如图①，在平面直角坐标系中，抛物线y=a（x﹣2）2﹣
经过原点O，与x轴的另一个交点为A，则a= ．
（2）【操作】将图①中抛物线在x轴下方的部分沿x轴折叠到x轴上方，将这部分图象与原抛物线剩余部分的图象组成的新图象记为G，如图②．直接写出图象G对应的函数解析式．
（3）【探究】在图②中，过点B（0，1）作直线l平行于x轴，与图象G的交点从左至右依次为点C，D，E，F，如图③．求图象G在直线l上方的部分对应的函数y随x增大而增大时x的取值范围．
（4）【应用】P是图③中图象G上一点，其横坐标为m，连接PD，PE．直接写出△PDE的面积不小于1时m的取值范围． -
科目： 来源： 题型：
查看答案和解析>>【题目】A地某厂和B地某厂同时制成机器若干台，A地某厂可支援外地10台，B地某厂可支援外地4台，现决定给C地8台，D地6台．已知从A运往D、C两地的运费分别是200元每台、400元每台，从B运往D、C两地的运费分别是150元每台、250元每台．
（1）设B地某厂运往D地x台，求总运费为多少元？
（2）在（1）中，当x＝2时，总运费是多少元？
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知：如图，在平面直角坐标系xOy中，正比例函数y=
x的图象经过点A，点A的纵坐标为4，反比例函数y= 
的图象也经过点A，第一象限内的点B在这个反比例函数的图象上，过点B作BC∥x轴，交y轴于点C，且AC=AB．求：
（1）这个反比例函数的解析式；
（2）直线AB的表达式． -
科目： 来源： 题型：
查看答案和解析>>【题目】某工厂现在平均每天比原计划多生产50台机器，现在生产600台机器所需要的时间与原计划生产450台机器所需要的时间相同．
（1）原计划平均每天生产多少台机器？
（2）若该工厂要在不超过5天的时间，生产1100台机器，则平均每天至少还要再多生产多少台机器？
-
科目： 来源： 题型：
查看答案和解析>>【题目】将两个大小不同的含30°角的三角板的直角顶点O重合在一起，保持△COD不动，将△AOB绕点O旋转，设射线AB与射线DC交于点F．
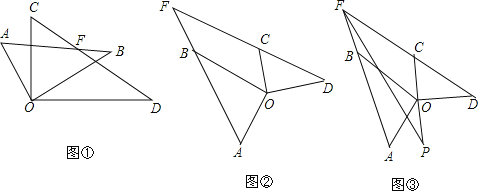
（1）如图①，若∠AOD=120°，
①AB与OD的位置关系 ．
②∠AFC的度数= ．
（2）如图②当∠AOD=130°，求∠AFC的度数．
（3）由上述结果，写出∠AOD和∠AFC的关系 ．
（4）如图③，作∠AFC、∠AOD的角平分线交于点P，求∠P的度数．
相关试题
