【题目】画出直线y=![]() x-1的图象,利用图象求:
x-1的图象,利用图象求:
(1)当x≥2时,y的取值范围;
(2)当y<0时,x的取值范围;
(3)当-1≤y≤2时,对应x的取值范围.
参考答案:
【答案】(1)当x≥2时,y≥0;(2)当y<0时,x<2;(3)当-1≤y≤2时,0≤x≤6.
【解析】
先利用两点确定直线y![]() 的图象.
的图象.
(1)观察函数图象得到当x≥2时,图象在x轴上方,则y≥0;
(2)观察图象得到当y<0时,图象在x轴下方,则x<2;
(3)观察图象得到当﹣1≤y≤2时,可得到0≤x≤6.
当x=2,y=0;当x=0,y=-1,过点(2,0)和(0,﹣1)画直线得到y![]() 的图象,如图,(1)当x≥2时,y≥0;
的图象,如图,(1)当x≥2时,y≥0;
(2)当y<0时,x<2;
(3)当﹣1≤y≤2时,0≤x≤6.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示的方格地面上,标有编号A,B,C的3个小方格地面是空地,另外6个小方格地面是草坪,除此以外小方格地面完全相同.

(1)一只自由飞行的鸟,将随意地落在图中的方格地面上,问小鸟落在草坪上的概率是多少?
(2)现从3个小方格空地中任意选取2个种植草坪,则刚好选取A和B的2个小方格空地种植草坪的概率是多少(用树形图或列表法求解)? -
科目: 来源: 题型:
查看答案和解析>>【题目】有一数值转换器,原理如图所示,若开始输入x的值是7,可发现第1次输出的结果是12,第2次输出的结果是6,第3次输出的结果是 ,依次继续下去…,第2013次输出的结果是 .
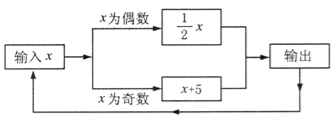
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠ACB=90°,∠A=45°,AB=4cm.点P从点A出发,以2cm/s的速度沿边AB向终点B运动.过点P作PQ⊥AB交折线ACB于点Q,D为PQ中点,以DQ为边向右侧作正方形DEFQ.设正方形DEFQ与△ABC重叠部分图形的面积是y(cm2),点P的运动时间为x(s).
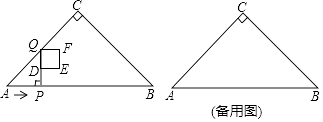
(1)当点Q在边AC上时,正方形DEFQ的边长为cm(用含x的代数式表示);
(2)当点P不与点B重合时,求点F落在边BC上时x的值;
(3)当0<x<2时,求y关于x的函数解析式;
(4)直接写出边BC的中点落在正方形DEFQ内部时x的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】为进一步普及我市中小学生的法律知识,提升学生法律意识,在2018年12月4日第五个国家宪法日来临之际,我市某区在中小学举行了“学习宪法”知识竞赛活动,各类获奖学生人数的比例情况如图所示,其中获得优胜奖的学生共400名,请结合图中信息,解答下列问题:
(1)求获得一等奖的学生人数;
(2)在本次知识竞赛活动中,A,B,C,D四所学校表现突出,现决定从这四所学校中随机选取两所学校举行一场法律知识抢答赛,请用画树状图或列表的方法求恰好选到A,B两所学校的概率.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知a、b、c在数轴上的位置如图所示,回答下列问题:
(1)化简:3|a﹣c|﹣2|﹣a﹣b|;
(2)令y=|x﹣a|+|x﹣b|+|x﹣c|,x满足什么条件时,y有最小值,求最小值

-
科目: 来源: 题型:
查看答案和解析>>【题目】《函数的图象与性质》拓展学习片段展示:
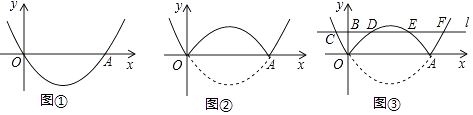
(1)【问题】如图①,在平面直角坐标系中,抛物线y=a(x﹣2)2﹣ 经过原点O,与x轴的另一个交点为A,则a= .
经过原点O,与x轴的另一个交点为A,则a= .
(2)【操作】将图①中抛物线在x轴下方的部分沿x轴折叠到x轴上方,将这部分图象与原抛物线剩余部分的图象组成的新图象记为G,如图②.直接写出图象G对应的函数解析式.
(3)【探究】在图②中,过点B(0,1)作直线l平行于x轴,与图象G的交点从左至右依次为点C,D,E,F,如图③.求图象G在直线l上方的部分对应的函数y随x增大而增大时x的取值范围.
(4)【应用】P是图③中图象G上一点,其横坐标为m,连接PD,PE.直接写出△PDE的面积不小于1时m的取值范围.
相关试题

