【题目】如图,两个反比例函数y1= ![]() (其中k1>0)和y2=
(其中k1>0)和y2= ![]() 在第一象限内的图象依次是C1和C2 , 点P在C1上,矩形PCOD交C2于A、B两点,OA的延长线交C1于点E,EF⊥x轴于F点,且图中四边形BOAP的面积为6,则EF:AC为 .
在第一象限内的图象依次是C1和C2 , 点P在C1上,矩形PCOD交C2于A、B两点,OA的延长线交C1于点E,EF⊥x轴于F点,且图中四边形BOAP的面积为6,则EF:AC为 . 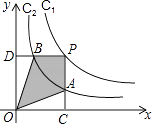
参考答案:
【答案】![]()
【解析】解:如图 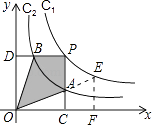 ,
,
∵B、C反比例函数y2= ![]() 的图象上,
的图象上,
∴S△ODB=S△OAC= ![]() ×3=
×3= ![]() ,
,
∵P在反比例函数y1= ![]() 的图象上,
的图象上,
∴S矩形PDOC=k1=6+ ![]() +
+ ![]() =9,
=9,
∴图象C1的函数关系式为y= ![]() ,
,
∵E点在图象C1上,
∴S△EOF= ![]() ×9=
×9= ![]() ,
,
∴ ![]() =
= ![]() =3,
=3,
∵AC⊥x轴,EF⊥x轴,
∴AC∥EF,
∴△EOF∽△AOC,
∴ ![]() =
= ![]() ,
,
所以答案是: ![]() .
.
【考点精析】本题主要考查了比例系数k的几何意义的相关知识点,需要掌握几何意义:表示反比例函数图像上的点向两坐标轴所作的垂线段与两坐标轴围成的矩形的面积才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,设点P到原点O的距离为ρ,OP与x轴正方向的交角为a,则用[ρ,a]表示点P的极坐标,例如:点P的坐标为(1,1),则其极坐标为[
 ,45°].若点Q的极坐标为[4,120°],则点Q的平面坐标为( )
,45°].若点Q的极坐标为[4,120°],则点Q的平面坐标为( ) 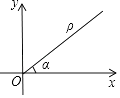
A.(﹣2,﹣2 )
)
B.(2,﹣2 )
)
C.(﹣2 ,﹣2)
,﹣2)
D.(﹣4,﹣4 )
) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,二次函数y=ax2+bx+c(a≠0)的图象与x轴交于点A、B两点,与y轴交于点C,对称轴为直线x=﹣1,点B的坐标为(1,0),则下列结论:①AB=4;②b2﹣4ac>0;③ab<0;④a2﹣ab+ac<0,其中正确的结论有( )个.

A.1个
B.2个
C.3个
D.4个 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知正方形ABCD的边长为4,点E、F分别在边AB、ABC上,且AE=BF=1,CE、DF相交于点O,下列结论: ①∠DOC=90°,②OC=OE,③tan∠OCD=
 ,④△COD的面积等于四边形BEOF的面积中,正确的有 ( )
,④△COD的面积等于四边形BEOF的面积中,正确的有 ( )
A.1个
B.2个
C.3个
D.4个 -
科目: 来源: 题型:
查看答案和解析>>【题目】计算:|﹣
 |+(2016﹣π)0﹣2sin45°+(
|+(2016﹣π)0﹣2sin45°+(  )﹣2 .
)﹣2 . -
科目: 来源: 题型:
查看答案和解析>>【题目】2017年深圳市男生体育中考考试项目为二项,在200米和1000米两个项目中选一个项目;另外在运球上篮、实心球、跳绳、引体向上四个项目中选一个.
(1)每位男考生一共有种不同的选择方案;
(2)若必胜,必成第一个项目都恰好选了200米,然后在第二组四个项目中各任意选取另外一个用画树状图或列表的方法求必胜和必成选择同种方案的概率. (友情提醒:各种方案可用A、B、C、…或①、②、③、…等符号来代表可简化解答过程) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一次函数y=ax+b(a≠0)的图形与反比例函数y=
 (k≠0)的图象交于第二、四象限内的A、B两点,与y轴交于C点,过点A作AH⊥y轴,垂足为H,OH=3,tan∠AOH=
(k≠0)的图象交于第二、四象限内的A、B两点,与y轴交于C点,过点A作AH⊥y轴,垂足为H,OH=3,tan∠AOH=  ,点B的坐标为(m,﹣2).
,点B的坐标为(m,﹣2). 
(1)求该反比例函数和一次函数的解析式.
(2)求△AOC的面积.
相关试题

