【题目】如图,一次函数y=ax+b(a≠0)的图形与反比例函数y= ![]() (k≠0)的图象交于第二、四象限内的A、B两点,与y轴交于C点,过点A作AH⊥y轴,垂足为H,OH=3,tan∠AOH=
(k≠0)的图象交于第二、四象限内的A、B两点,与y轴交于C点,过点A作AH⊥y轴,垂足为H,OH=3,tan∠AOH= ![]() ,点B的坐标为(m,﹣2).
,点B的坐标为(m,﹣2). 
(1)求该反比例函数和一次函数的解析式.
(2)求△AOC的面积.
参考答案:
【答案】
(1)解:∵OH=3,tan∠AOH= ![]() ,
,
∴AH=OHtan∠AOH=4,
∴点A的坐标为(﹣4,3).
∵点A在反比例函数y= ![]() (k≠0)的图象上,
(k≠0)的图象上,
∴k=﹣4×3=﹣12,
∴反比例函数解析式为y=﹣ ![]() .
.
∵点B(m,﹣2)在反比例函数y=﹣的图象上,
∴m=﹣ ![]() =6,
=6, ![]()
∴点B的坐标为(6,﹣2).
将A(﹣4,3)、B(6,﹣2)代入y=ax+b,
![]() ,解得:
,解得: 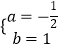 ,
,
∴一次函数的解析式为y=﹣ ![]() x+1.
x+1.
(2)解:当x=0时,y=﹣ ![]() x+1=1,
x+1=1,
∴点C的坐标为(0,1),
∴OC=1,
∴S△AOC= ![]() OCAH=
OCAH= ![]() ×1×4=2.
×1×4=2.
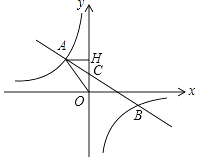
【解析】(1)由OH和tan∠AOH的值即可求出点A的坐标,利用反比例函数图象上点的坐标特征即可求出k值和点B的坐标,再根据点A、B的坐标利用待定系数法即可求出直线AB的解析式;(2)将x=0代入直线AB的解析式中求出y值,由此即可得出OC的长度,再根据三角形的面积公式即可求出△AOC的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,两个反比例函数y1=
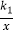 (其中k1>0)和y2=
(其中k1>0)和y2= 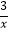 在第一象限内的图象依次是C1和C2 , 点P在C1上,矩形PCOD交C2于A、B两点,OA的延长线交C1于点E,EF⊥x轴于F点,且图中四边形BOAP的面积为6,则EF:AC为 .
在第一象限内的图象依次是C1和C2 , 点P在C1上,矩形PCOD交C2于A、B两点,OA的延长线交C1于点E,EF⊥x轴于F点,且图中四边形BOAP的面积为6,则EF:AC为 . 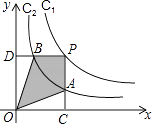
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:|﹣
 |+(2016﹣π)0﹣2sin45°+(
|+(2016﹣π)0﹣2sin45°+(  )﹣2 .
)﹣2 . -
科目: 来源: 题型:
查看答案和解析>>【题目】2017年深圳市男生体育中考考试项目为二项,在200米和1000米两个项目中选一个项目;另外在运球上篮、实心球、跳绳、引体向上四个项目中选一个.
(1)每位男考生一共有种不同的选择方案;
(2)若必胜,必成第一个项目都恰好选了200米,然后在第二组四个项目中各任意选取另外一个用画树状图或列表的方法求必胜和必成选择同种方案的概率. (友情提醒:各种方案可用A、B、C、…或①、②、③、…等符号来代表可简化解答过程) -
科目: 来源: 题型:
查看答案和解析>>【题目】黄岩岛自古以来就是中国的领土,如图,为维护海洋利益,三沙市一艘海监船在黄岩岛附近海域巡航,某一时刻海监船在A处测得该岛上某一目标C在它的北偏东45°方向,海监船以30海里每小时的速度沿北偏西30°方向航行2小时后到达B处,此时测得该目标C在它的南偏东75°方向.求:

(1)∠C的度数;
(2)求该船与岛上目标C之间的距离 即CB的长度(结果保留根号) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点F在ABCD的对角线AC上,过点F、B分别作AB、AC的平行线相交于点E,连接BF,∠ABF=∠FBC+∠FCB.

(1)求证:四边形ABEF是菱形;
(2)若BE=5,AD=8,sin∠CBE= ,求AC的长.
,求AC的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知抛物线y=
 x2+bx+c经过△ABC的三个顶点,其中点A(0,1),点B(﹣9,10),AC∥x轴,点P是直线AC下方抛物线上的动点.
x2+bx+c经过△ABC的三个顶点,其中点A(0,1),点B(﹣9,10),AC∥x轴,点P是直线AC下方抛物线上的动点.
(1)求抛物线的解析式;
(2)过点P且与y轴平行的直线l与直线AB、AC分别交于点E、F,当四边形AECP的面积最大时,求点P的坐标;
(3)当点P为抛物线的顶点时,在直线AC上是否存在点Q,使得以C、P、Q为顶点的三角形与△ABC相似,若存在,求出点Q的坐标,若不存在,请说明理由.
相关试题

