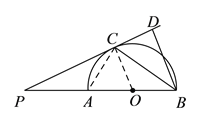
【题目】如图, ![]() 是半圆
是半圆![]() 的直径,点
的直径,点![]() 是
是![]() 延长线上 一点,
延长线上 一点, ![]() 是⊙
是⊙![]() 的切线,切点为
的切线,切点为![]() ,过点
,过点![]() 作
作![]() 交
交![]() 的延长线于点
的延长线于点![]() ,连接
,连接![]() .求证:
.求证:
(![]() )
)![]() .
.
(![]() )
)![]() .
.

参考答案:
【答案】(1)证明见解析;(2)证明见解析.
【解析】试题分析:(1)连接OC,由PC为⊙![]() 的切线,利用切线的性质得到OC⊥PC,再由BD⊥PD,得到一对直角相等,利用同位角相等两直线平行得到OC与BD平行,进而得到一对内错角相等,再由OB=OC,利用等边对等角得到一对角相等,等量代换即可得证;
的切线,利用切线的性质得到OC⊥PC,再由BD⊥PD,得到一对直角相等,利用同位角相等两直线平行得到OC与BD平行,进而得到一对内错角相等,再由OB=OC,利用等边对等角得到一对角相等,等量代换即可得证;
(2)连接AC,由AB为⊙![]() 的直径,利用圆周角定理得到∠ACB为直角,利用两对角相等的三角形相似得到△ABC与△CBD相似,利用相似三角形对应边成比例,变形即可得证.
的直径,利用圆周角定理得到∠ACB为直角,利用两对角相等的三角形相似得到△ABC与△CBD相似,利用相似三角形对应边成比例,变形即可得证.
证明:(![]() )连接
)连接![]() ,
,
∵![]() 与圆
与圆![]() 相切,
相切,
∴![]() ,即
,即![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ;
;
(![]() )连接
)连接![]() ,
,
∵![]() 为圆
为圆![]() 的直径,
的直径,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
则![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了参加“醴陵市中小学生首届诗词大会”,某中学八年级的两班学生进行了预选,其中班上前5名学生的成绩(百分制)分别为:八(1)班86,85,77 ,92, 85;八(2)班79 ,85 ,92,85 ,89.通过数据分析,列表如下:
班级
平均分
中位数
众数
方差
八(1)
85
b
c
d
八(2)
a
85
85
e
(1)直接写出表中a,b,c的值:a= ,b= ,c= .
(2)求d,e的值,并根据以上数据分析,你认为哪个班前5名同学的成绩较好?说明理由.
(3)若“醴陵市中小学生首届诗词大会”中,各中学代表队成绩计分分两部分:现场评委记分和网络评委投票记分。且现场评委记分权数为80%,网络评委投票记分权数为20%,请计算A,B,C三所中学代表队的最终得分为多少?
中学A
中学B
中学C
评委记分
90
80
85
网络投票记分
85
92
88
-
科目: 来源: 题型:
查看答案和解析>>【题目】填空并完成以下证明:
已知:点P在直线CD上,∠BAP+∠APD=180°,∠1=∠2.
求证:AB∥CD,∠E=∠F.
证明:∵∠BAP+∠APD=180°,(已知)
∴AB∥ .( )
∴∠BAP= .( )
又∵∠1=∠2,(已知)
∠3= ﹣∠1,
∠4= ﹣∠2,
∴∠3= (等式的性质)
∴AE∥PF.( )
∴∠E=∠F.( )

-
科目: 来源: 题型:
查看答案和解析>>【题目】为了传承优秀传统文化,某校开展“经典诵读”比赛活动,诵读材料有《论语》,《三字经》,《弟子规》(分别用字母A,B,C依次表示这三个诵读材料),将A,B,C这三个字母分别写在3张完全相同的不透明卡片的正面上,把这3张卡片背面朝上洗匀后放在桌面上.小明和小亮参加诵读比赛,比赛时小明先从中随机抽取一张卡片,记录下卡片上的内容,放回后洗匀,再由小亮从中随机抽取一张卡片,选手按各自抽取的卡片上的内容进行诵读比赛.
(1)小明诵读《论语》的概率是 .
(2)请用列表法或画树状图法求小明和小亮诵读两个不同材料的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:∠A=(90+x)°,∠B=(90﹣x)°,∠CED=90°,射线EF∥AC,2∠C﹣∠D=m.(1)判断AC与BD的位置关系,并说明理由.
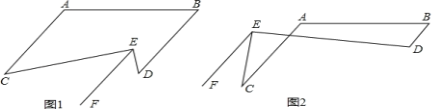
(2)如图1,当m=30°时,求∠C、∠D的度数.
(3)如图2,求∠C、∠D的度数(用含m的代数式表示).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
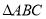 中,
中,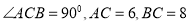 .点
.点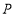 从点
从点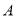 出发沿
出发沿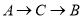 路径向终点
路径向终点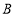 运动;点
运动;点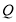 从
从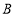 点出发沿
点出发沿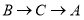 路径向终点
路径向终点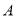 运动.点
运动.点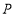 和
和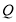 分别以1和3的运动速度同时开始运动,两点都要到相应的终点时才能停止运动,在某时刻,分别过
分别以1和3的运动速度同时开始运动,两点都要到相应的终点时才能停止运动,在某时刻,分别过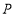 和
和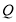 作
作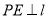 于
于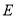 ,
,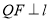 于
于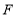 .则点
.则点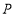 运动时间等于____________时,
运动时间等于____________时,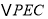 与
与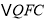 全等。
全等。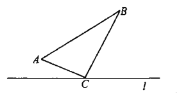
-
科目: 来源: 题型:
查看答案和解析>>【题目】画图并填空:如图,方格纸中每个小正方形的边长都为1.在方格纸内将△ABC经过一次平移后得到△A′B′C′,图中标出了点B的对应点B′.
(1)在给定方格纸中画出平移后的△A′B′C′;
(2)画出AB边上的中线CD
(3)画出BC边上的高线AE
(4)点
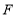 为方格纸上的格点(异于点
为方格纸上的格点(异于点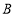 ),若
),若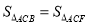 ,则图中的格点
,则图中的格点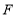 共有 个.
共有 个.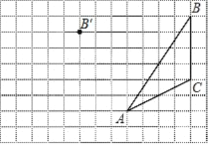
相关试题

