【题目】已知:∠A=(90+x)°,∠B=(90﹣x)°,∠CED=90°,射线EF∥AC,2∠C﹣∠D=m.(1)判断AC与BD的位置关系,并说明理由.
(2)如图1,当m=30°时,求∠C、∠D的度数.
(3)如图2,求∠C、∠D的度数(用含m的代数式表示).
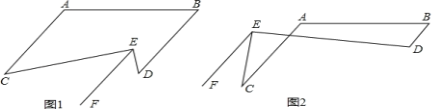
参考答案:
【答案】(1)AC∥BD,理由见解析;(2)∠C=40°,∠D=50°;(3)∠C=90°+m,∠D=180°+m
【解析】
(1)根据同旁内角互补两直线平行求出AC∥BD;
(2)根据两直线平行,内错角相等可得∠CEF=∠C,∠DEF=∠D,然后列出关于∠C、∠D的二元一次方程组求解即可;
(3)根据两直线平行,内错角相等可得∠CEF=∠C,∠DEF=∠D,再根据∠CED=∠DEF-∠CEF得到∠D-∠C=90°,然后求解即可.
(1)∵∠A+∠B=(90+x)°+(90x)°=180°,
∴AC∥BD
(2)∵EF∥AC,
∴AC∥EF∥BD,
∴∠CEF=∠C,∠DEF=∠D,
∵∠CED=90,
∴∠C+∠D=90,
联立
![]() ,
,
解得![]()
(3)∵EF∥AC,
∴AC∥EF∥BD,
∴∠CEF=∠C,∠DEF=∠D,
∵∠CED=∠DEF-∠CEF=90°,
∴∠D-∠C=90°,①
又2∠C∠D=m ②
联立,① ②
解得∠C=90°+m,∠D=180°+m
-
科目: 来源: 题型:
查看答案和解析>>【题目】填空并完成以下证明:
已知:点P在直线CD上,∠BAP+∠APD=180°,∠1=∠2.
求证:AB∥CD,∠E=∠F.
证明:∵∠BAP+∠APD=180°,(已知)
∴AB∥ .( )
∴∠BAP= .( )
又∵∠1=∠2,(已知)
∠3= ﹣∠1,
∠4= ﹣∠2,
∴∠3= (等式的性质)
∴AE∥PF.( )
∴∠E=∠F.( )

-
科目: 来源: 题型:
查看答案和解析>>【题目】为了传承优秀传统文化,某校开展“经典诵读”比赛活动,诵读材料有《论语》,《三字经》,《弟子规》(分别用字母A,B,C依次表示这三个诵读材料),将A,B,C这三个字母分别写在3张完全相同的不透明卡片的正面上,把这3张卡片背面朝上洗匀后放在桌面上.小明和小亮参加诵读比赛,比赛时小明先从中随机抽取一张卡片,记录下卡片上的内容,放回后洗匀,再由小亮从中随机抽取一张卡片,选手按各自抽取的卡片上的内容进行诵读比赛.
(1)小明诵读《论语》的概率是 .
(2)请用列表法或画树状图法求小明和小亮诵读两个不同材料的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
 是半圆
是半圆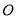 的直径,点
的直径,点 是
是 延长线上 一点,
延长线上 一点,  是⊙
是⊙ 的切线,切点为
的切线,切点为 ,过点
,过点 作
作 交
交 的延长线于点
的延长线于点 ,连接
,连接 .求证:
.求证:(
 )
) .
.(
 )
) .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
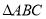 中,
中,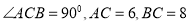 .点
.点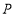 从点
从点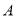 出发沿
出发沿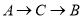 路径向终点
路径向终点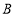 运动;点
运动;点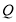 从
从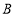 点出发沿
点出发沿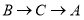 路径向终点
路径向终点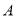 运动.点
运动.点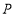 和
和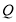 分别以1和3的运动速度同时开始运动,两点都要到相应的终点时才能停止运动,在某时刻,分别过
分别以1和3的运动速度同时开始运动,两点都要到相应的终点时才能停止运动,在某时刻,分别过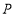 和
和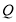 作
作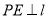 于
于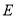 ,
,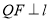 于
于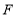 .则点
.则点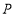 运动时间等于____________时,
运动时间等于____________时,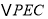 与
与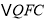 全等。
全等。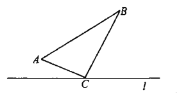
-
科目: 来源: 题型:
查看答案和解析>>【题目】画图并填空:如图,方格纸中每个小正方形的边长都为1.在方格纸内将△ABC经过一次平移后得到△A′B′C′,图中标出了点B的对应点B′.
(1)在给定方格纸中画出平移后的△A′B′C′;
(2)画出AB边上的中线CD
(3)画出BC边上的高线AE
(4)点
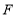 为方格纸上的格点(异于点
为方格纸上的格点(异于点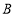 ),若
),若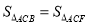 ,则图中的格点
,则图中的格点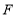 共有 个.
共有 个.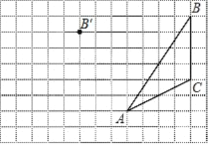
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校计划组织师生共435人参加一次大型公益活动,如果租用5辆小客车和6辆大客车恰好全部坐满,已知每辆大客车的乘客座位数比小客车多12个.
(1) 求每辆小客车和每辆大客车的乘客座位数;
(2) 由于最后参加活动的人数增加了20人,学校决定调整租车方案,在保持租用车辆总数不变的情况下,为将所有参加活动的师生装载完成,求租用小客车数量的最大值.
相关试题

