【题目】为了传承优秀传统文化,某校开展“经典诵读”比赛活动,诵读材料有《论语》,《三字经》,《弟子规》(分别用字母A,B,C依次表示这三个诵读材料),将A,B,C这三个字母分别写在3张完全相同的不透明卡片的正面上,把这3张卡片背面朝上洗匀后放在桌面上.小明和小亮参加诵读比赛,比赛时小明先从中随机抽取一张卡片,记录下卡片上的内容,放回后洗匀,再由小亮从中随机抽取一张卡片,选手按各自抽取的卡片上的内容进行诵读比赛.
(1)小明诵读《论语》的概率是 .
(2)请用列表法或画树状图法求小明和小亮诵读两个不同材料的概率.
参考答案:
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】试题分析:(1)直接根据概率公式求解;
(2)利用列表法展示所有9种等可能性结果,再找出小华和小敏诵读两个不同材料的结果数,然后根据概率公式求解.
试题解析:(1)小华诵读《弟子规》的概率=![]() ;
;
(2)列表得:
小华 | A | B | C |
A | (A,A) | (A,B) | (A,C) |
B | (B,A) | (B,B) | (B,C) |
C | (C,A) | (C,B) | (C,C) |
由表格可知,共有9种等可能性结果,其中小华和小敏诵读两个不同材料的结果有6种,
所以P(小华和小敏诵读两个不同材料)=![]() .
.
-
科目: 来源: 题型:
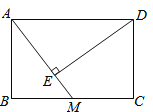
查看答案和解析>>【题目】如图,在矩形ABCD中,AB=2,BC=3,M为BC中点,连接AM,过D作DE⊥AM于E,则DE的长度为_______________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】【阅读理解】对于任意正实数a、b,
∵(
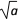 -
-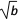 )2≥0,∴a-2
)2≥0,∴a-2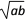 +b≥0,
+b≥0,∴a+b≥2
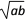 ,(只有当a=b时,a+b等于2
,(只有当a=b时,a+b等于2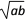 ).
).【获得结论】在a+b≥2
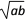 (a、b均为正实数)中,若ab为定值p,
(a、b均为正实数)中,若ab为定值p,则a+b≥2
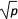 ,只有当a=b时,a+b有最小值2
,只有当a=b时,a+b有最小值2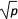 .
.根据上述内容,回答下列问题:(1)若
 >0,只有当
>0,只有当 = 时,m+
= 时,m+ 有最小值 .
有最小值 . 【探索应用】(2)已知点Q(-3,-4)是双曲线y=
 上一点,过Q作QA⊥x轴于点A,作QB⊥y轴于点B.点P为双曲线y=
上一点,过Q作QA⊥x轴于点A,作QB⊥y轴于点B.点P为双曲线y= (x>0)上任意一点,连接PA,PB,求四边形AQBP的面积的最小值.
(x>0)上任意一点,连接PA,PB,求四边形AQBP的面积的最小值. 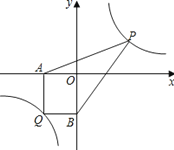
-
科目: 来源: 题型:
查看答案和解析>>【题目】放大镜中的四边形与原四边形的关系是( )
A. 平移B. 相似C. 旋转D. 成轴对称
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个三角形的三个内角的度数比是1 ∶6 ∶5 ,最大的一个内角是__________度,按角分,它是一个________角三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】两个整数的和是60,它们的最小公倍数是273,则这两个整数的乘积是( )
A. 273 B. 819 C. 1911 D. 3549
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列图形中,不一定是轴对称图形的是( )
A. 圆 B. 长方形 C. 等腰三角形 D. 直角三角形
相关试题

