【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,以线段
,以线段![]() 为边向外作等边
为边向外作等边![]() ,点
,点![]() 是线段
是线段![]() 的中点,连结
的中点,连结![]() 并延长交线段
并延长交线段![]() 于点
于点![]() .
.
(1)求证:四边形![]() 为平行四边形;
为平行四边形;
(2)求平行四边形![]() 的面积;
的面积;
(3)如图,分别作射线![]() ,
,![]() ,如图中
,如图中![]() 的两个顶点
的两个顶点![]() ,
,![]() 分别在射线
分别在射线![]() ,
,![]() 上滑动,在这个变化的过程中,求出线段
上滑动,在这个变化的过程中,求出线段![]() 的最大长度.
的最大长度.

参考答案:
【答案】(1)证明见解析;(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1)在Rt△ABC中,E为AB的中点,则CE=![]() AB,BE=
AB,BE=![]() AB,得到∠BCE=∠EBC=60°.由△AEF≌△BEC,得∠AFE=∠BCE=60°.又∠D=60°,得∠AFE=∠D=60度.所以FC∥BD,又因为∠BAD=∠ABC=60°,所以AD∥BC,即FD∥BC,则四边形BCFD是平行四边形;
AB,得到∠BCE=∠EBC=60°.由△AEF≌△BEC,得∠AFE=∠BCE=60°.又∠D=60°,得∠AFE=∠D=60度.所以FC∥BD,又因为∠BAD=∠ABC=60°,所以AD∥BC,即FD∥BC,则四边形BCFD是平行四边形;
(2)在Rt△ABC中,求出BC,AC即可解决问题;
(3)取![]() 的中点
的中点![]() ,连结
,连结![]() ,
,![]() ,
,![]() ,根据三角形三边关系进行求解即可得.
,根据三角形三边关系进行求解即可得.
(1)在![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,
在等边![]() 中,
中,![]() ,
,![]() ,
,
![]() 为
为![]() 的中点,
的中点,![]() ,
,
又![]() ,
,
![]() ,
,
在![]() 中,
中,![]() ,
,![]() 为
为![]() 的中点,
的中点,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() ,
,
又![]() ,
,![]() ,
,
又![]() ,
,![]() ,
,
![]() ,
,
又![]() ,
,![]() ,即
,即![]() ,
,
![]() 四边形
四边形![]() 是平行四边形;
是平行四边形;
(2)在![]() 中,
中,![]() ,
,![]() ,
,
![]() ,
,
∴![]()
![]()
![]() ,
,
![]() ;
;
(3)取![]() 的中点
的中点![]() ,连结
,连结![]() ,
,![]() ,
,![]()
![]() ,
,
![]() 的最大长度
的最大长度![]() .
.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某社区要调查社区居民双休日的学习状况,采用下列调查方式:

①从一幢高层住宅楼中选取200名居民;
②从不同住宅楼中随机选取200名居民;
③选取社区内200名在校学生.
(1)上述调查方式最合理的是 ;
(2)将最合理的调查方式得到的数据制成扇形统计图(如图1)和频数分布直方图(如图2),在这个调查中,200名居民双休日在家学习的有 人;
(3)请估计该社区2 000名居民双休日学习时间不少于4小时的人数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平行四边形ABCD中,连接BD,且BD=CD,过点A作AM⊥BD于点M,过点D作DN⊥AB于点N,且DN=
 ,在DB的延长线上取一点P,满足∠ABD=∠MAP+∠PAB,则AP=_____.
,在DB的延长线上取一点P,满足∠ABD=∠MAP+∠PAB,则AP=_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知点A(1,a)是反比例函数
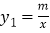 的图象上一点,直线
的图象上一点,直线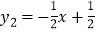 与反比例函数
与反比例函数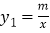 的图象的交点为点B、D,且B(3,﹣1),求:
的图象的交点为点B、D,且B(3,﹣1),求:(1)求反比例函数的解析式;
(2)求点D坐标,并直接写出y1>y2时x的取值范围;
(3)动点P(x,0)在x轴的正半轴上运动,当线段PA与线段PB之差达到最大时,求点P的坐标.

-
科目: 来源: 题型:
查看答案和解析>>【题目】一辆汽车从A地驶往B地,前
 路段为普通公路,其余路段为高速公路.已知汽车在普通公路上行驶的速度为60km/h,在高速公路上行驶的速度为100km/h,汽车从A地到B地一共行驶了2.2h.
路段为普通公路,其余路段为高速公路.已知汽车在普通公路上行驶的速度为60km/h,在高速公路上行驶的速度为100km/h,汽车从A地到B地一共行驶了2.2h.请你根据以上信息,就该汽车行驶的“路程”或“时间”,提出一个用一元一次方程解决的问题,并写出解答过程.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形BCDE的各边分别平等于x轴或y轴,物体甲和物体乙分别由点A(2,0)同时出发,沿矩形BCDE的边作环绕运动,物体甲按逆时针方向以1个单位/秒匀速运动,物体乙按顺时针方向以2个单位/秒匀速运动,则两个物体运动后第2015次相遇地点的坐标是( )
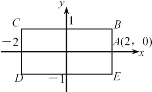
A. (2,0)B. (-1,-1)C. (-2,1)D. (-1,1)
-
科目: 来源: 题型:
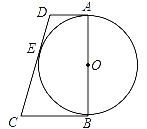
查看答案和解析>>【题目】如图所示,AB是⊙O的直径,AD与⊙O相切于点A,DE与⊙O相切于点E,点C为DE延长线上一点,且CE=CB.
(1)求证:BC为⊙O的切线;
(2)若AB=4,AD=1,求线段CE的长.
相关试题

