【题目】一辆货车和一辆小轿车同时从甲地出发,货车匀速行驶至乙地,小轿车中途停车休整后提速行驶至乙地,货车行驶的路程y1(km),小轿车行驶的路程y2(km)与时间x(h)的对应关系如图所示,下列结论错误的是( )

A. 甲、乙两地相距420km
B. y1=60x,y2=![]()
C. 货车出发4.5h与小轿车首次相遇
D. 两车首次相遇时距乙地150km
参考答案:
【答案】B
【解析】(1)直接根据图象写出两地之间的距离;
(2)分别利用待定系数法确定函数的解析式即可;
(3)首先求出乙行驶路程的函数关系式,进而利用0<x≤3,得出答案即可.
(4)火车在3≤x≤5时,会与小轿车相遇。
(2)①y1=60x(0≤x≤7);
②当x=5.75时,y1=60×5.75=345,
x≥5时,设y2=kx+b,
∵y2的图象经过(5.75,345),(6.5,420),
∴![]() ,
,
解得:![]() ,
,
∴x≥5时,y2=100x-230;
当x=5时,y=100×5-230=270,
∴小车速度是90km/h,即当x<3时,y2=90x
当3时,y2=270
故y2= ,故选项B错误;
,故选项B错误; ![]()
(3)x=5时,y=100×5-230=270,即小轿车在3≤x≤5停车休整,离甲地270km,
当x=3时,y1=180;x=5时,y1=300,
∴火车在3≤x≤5时,会与小轿车相遇,
即270=60x,x=4.5;
当0<x≤3时,小轿车的速度为270÷3=90km/h,
而货车速度为60km/h,
故货车在0<x≤3时,不会与小轿车相遇,
∴货车出发4.5小时后首次与小轿车相遇,距离甲地270km,距乙地150km.故选项C,D正确.
故选:B
-
科目: 来源: 题型:
查看答案和解析>>【题目】小王计划租一间商铺,下面是某房屋中介提供的两种商铺的出租信息:

设租期为x(月),所需租金为y(元),其中x为大于1的整数.
(1)若小王计划租用的商铺为90m2,请分别写出在商座A,B租商铺所需租金yA(元),yB(元)与租期x(月)之间的函数关系式;
(2)在(1)的前提下,请你帮助小王根据租期,租用哪个商座的商铺房租更低.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,已知点A(0,2),△AOB为等边三角形,P是x轴上一个动点(不与原O重合),以线段AP为一边在其右侧作等边三角形△APQ.

(1)求点B的坐标;
(2)在点P的运动过程中,∠ABQ的大小是否发生改变?如不改变,求出其大小;如改变,请说明理由.
(3)连接OQ,当OQ∥AB时,求P点的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,已知抛物线y=ax2+bx﹣2(a≠0)与x轴交于A(1,0)、B(3,0)两点,与y轴交于点C,其顶点为D.
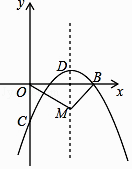
(1)求抛物线的解析式;
(2)一动点M从点D出发,以每秒1个单位的速度沿抛物线的对称轴向下运动,连OM,BM,设运动时间为t秒(t=0),在点M的运动过程中,当∠OMB=90°时,求t的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,△ABC与△CDE是等腰直角三角形,直角边AC、CD在同一条直线上,点M,N分别是斜边AB,DE的中点,点P为AD的中点,连接AE、BD、MN.
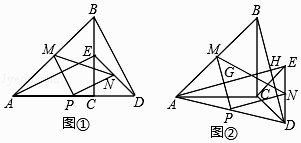
(1)求证:△PMN为等腰直角三角形;
(2)现将图①中的△CDE绕着点C顺时针旋转α(0°<α<90°),得到图②,AE与MP,BD分别交于点G、H,请判断①中的结论是否成立,若成立,请证明;若不成立,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】下列各运算中,计算正确的是( )
A.(﹣3ab2)2=9a2b4
B.2a+3b=5ab
C. =±3
=±3
D.(a﹣b)2=a2﹣b2 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线y=x+1分别与x轴、y轴相交于点A、B,以点A为圆心、AB长为半径画弧交x轴于点A1,再过点A1作x轴的垂线交直线于点B1,以点A为圆心、AB1长为半径画弧交x轴于点A2……按此做法进行下去,则点A8的坐标是________.
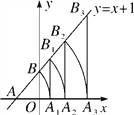
相关试题

