【题目】已知二次函数y=x2+bx+c(b,c为常数).
(1)当b=2,c=﹣3时,求二次函数图象的顶点坐标;
(2)当c=10时,若在函数值y=1的情况下,只有一个自变量x的值与其对应,求此时二次函数的解析式;
(3)当c=b2时,若在自变量x的值满足b≤x≤b+3的情况下,与其对应的函数值y的最小值为21,求此时二次函数的解析式.
参考答案:
【答案】
(1)解:当b=2,c=﹣3时,二次函数的解析式为y=x2+2x﹣3=(x+1)2﹣4,
故当x=﹣1时,二次函数取得最小值﹣4
(2)解:当c=10时,二次函数的解析式为y=x2+bx+10,
由题意得,x2+bx+10=1有两个相等是实数根,
∴△=b2﹣36=0,
解得b1=6,b2=﹣6,
∴二次函数的解析式y=x2+6x+10,y=x2﹣6x+10
(3)解:当c=b2时,二次函数解析式为y═x2+bx+b2,
图象开口向上,对称轴为直线x=﹣ ![]() ,
,
①当﹣ ![]() <b,即b>0时,
<b,即b>0时,
在自变量x的值满足b≤x≤b+3的情况下,y随x的增大而增大,
∴当x=b时,y=b2+bb+b2=3b2为最小值,
∴3b2=21,解得b1=﹣ ![]() (舍去),b2=
(舍去),b2= ![]() ;
;
②当b≤﹣ ![]() ≤b+3时,即﹣2≤b≤0,
≤b+3时,即﹣2≤b≤0,
∴x=﹣ ![]() ,y=
,y= ![]() b2为最小值,
b2为最小值,
∴ ![]() b2=21,解得b1=﹣2
b2=21,解得b1=﹣2 ![]() (舍去),b2=2
(舍去),b2=2 ![]() (舍去);
(舍去);
③当﹣ ![]() >b+3,即b<﹣2,
>b+3,即b<﹣2,
在自变量x的值满足b≤x≤b+3的情况下,y随x的增大而减小,
故当x=b+3时,y=(b+3)2+b(b+3)+b2=3b2+9b+9为最小值,
∴3b2+9b+9=21.解得b1=1(舍去),b2=﹣4;
∴b= ![]() 时,解析式为:y=x2+
时,解析式为:y=x2+ ![]() x+7
x+7
b=﹣4时,解析式为:y=x2﹣4x+16.
综上可得,此时二次函数的解析式为y=x2+ ![]() x+7或y=x2﹣4x+16
x+7或y=x2﹣4x+16
【解析】(1)把b=2,c=﹣3代入函数解析式,求二次函数的最小值;(2)根据当c=10时,若在函数值y=l的情况下,只有一个自变量x的值与其对应,得到x2+bx+5=1有两个相等是实数根,求此时二次函数的解析式;(3)当c=b2时,写出解析式,分三种情况进行讨论即可.
【考点精析】掌握二次函数的最值是解答本题的根本,需要知道如果自变量的取值范围是全体实数,那么函数在顶点处取得最大值(或最小值),即当x=-b/2a时,y最值=(4ac-b2)/4a.
-
科目: 来源: 题型:
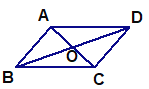
查看答案和解析>>【题目】如图,在四边形ABCD中,对角线AC、BD相交于点O,其中AC+BD=14,CD=5.
(1)若四边形ABCD是平行四边形,则△OCD的周长为_____________;
(2) 若四边形ABCD是矩形,则AD的长为_____________;
(3) 若四边形ABCD是菱形,则菱形的面积为___________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】把下列各数填在相应的集合内:
100,﹣0.82,﹣30
 ,3.14,﹣2,0,﹣2011,﹣3.1
,3.14,﹣2,0,﹣2011,﹣3.1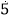 ,
, ,﹣
,﹣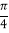 ,2.010010001…,
,2.010010001…,正分数集合:{ …}
整数集合:{ …}
负有理数集合:{ …}
非正整数集合;{ …}
无理数集合:{ …}.
-
科目: 来源: 题型:
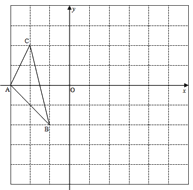
查看答案和解析>>【题目】如图,图中的小方格都是边长为1的正方形,△ABC的顶点坐标分别为:A(-3,0),B(-1,-2),C(-2,2).
(1)请在图中画出△ABC绕B点顺时针旋转90°后的图形△A′BC′.
(2)请直接写出以A′、B、C′为顶点平行四边形的第4个顶点D的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知在纸面上有一数轴(如图),折叠纸面.例如:若数轴上数2表示的点与数﹣2表示的点重合,则数轴上数﹣4表示的点与数4表示的点重合,根据你对例题的理解,解答下列问题:

若数轴上数﹣3表示的点与数1表示的点重合.(根据此情境解决下列问题)
①则数轴上数3表示的点与数_______________表示的点重合.
②若点A到原点的距离是5个单位长度,并且A、B两点经折叠后重合,则B点表示的数是_________.
③若数轴上M、N两点之间的距离为2010,并且M、N两点经折叠后重合,
如果M点表示的数比N点表示的数大,则M点表示的数是________.则N点
表示的数是________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】矩形ABCD的两条对称轴为坐标轴,点A的坐标为(2,1).一张透明纸上画有一个点和一条抛物线,平移透明纸,这个点与点A重合,此时抛物线的函数表达式为y=x2 , 再次平移透明纸,使这个点与点C重合,则该抛物线的函数表达式变为( )
A.y=x2+8x+14
B.y=x2-8x+14
C.y=x2+4x+3
D.y=x2-4x+3 -
科目: 来源: 题型:
查看答案和解析>>【题目】某中学开展了“手机伴我健康行”主题活动.他们随机抽取部分学生进行“手机使用目的”和“每周使用手机时间”的问卷调查,并绘制成如图①②的统计图。已知“查资料”人人数是40人。

请你根据以上信息解答以下问题
(1)在扇形统计图中,“玩游戏”对应的圆心角度数是_______________。
(2)补全条形统计图
(3)该校共有学生1200人,估计每周使用手机时间在2小时以上(不含2小时)的人数
相关试题

