搜索
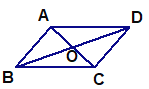
【题目】如图，在四边形ABCD中，对角线AC、BD相交于点O，其中AC+BD=14，CD=5．
(1)若四边形ABCD是平行四边形，则△OCD的周长为_____________；
(2) 若四边形ABCD是矩形，则AD的长为_____________；
(3) 若四边形ABCD是菱形，则菱形的面积为___________．
参考答案：
【答案】 12， 
， 24
【解析】分析：(1)根据平行四边形性质求出OD+OC即可求出答案;
(2)根据矩形性质求出AC,根据勾股定理求出即可;
(3)根据矩形性质求出OD+OC,根据勾股定理求出OC×OD,进一步求出AC×BD,即可求出面积.
详解：(1) ∵四边形ABCD是平行四边形,
, 
,
,
,
的周长为
,
故答案为:12.
(2)
矩形ABCD,
,
,
由勾股定理得: 
,
故答案为: ;
(3) 
, 四边形ABCD是菱形,
由勾股定理得:
,
,
,
,
∴菱形的面积为是
,
故答案为:24.
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图所示，圆的周长为4个单位长度，在圆的4等分点处标上数字0，1，2，3，先让圆周上数字0所对应的点与数轴上的数－2所对应的点重合，再让圆沿着数轴按顺时针方向滚动，那么数轴上的数－2017将与圆周上的哪个数字重合（ ）
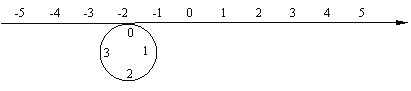
A. 0 B. 1 C. 2 D. 3
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在平面直角坐标系中，四边形ABCD为正方形，已知点A（﹣6，0），D（﹣7，3），点B、C在第二象限内．
（1）求点B的坐标。
（2）将正方形ABCD以每秒1个单位的速度沿x轴向右平移t秒，若存在某一时刻t，使在第一象限内点B、D两点的对应点B′、D′正好落在某反比例函数的图象上，请求出此时t的值以及这个反比例函数的解析式；
（3）在（2）的情况下，问是否存在x轴上的点P和反比例函数图象上的点Q，使得以P、Q、B′、D′四个点为顶点的四边形是平行四边形？若存在，请直接写出符合题意的点P、Q的坐标；若不存在，请说明理由．
-
科目： 来源： 题型：
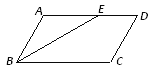
查看答案和解析>>【题目】平行四边形ABCD中，∠ABC的角平分线BE将边AD分成长度为5cm和6cm的两部分，则平行四边形ABCD的周长为__________________cm．
-
科目： 来源： 题型：
查看答案和解析>>【题目】把下列各数填在相应的集合内：
100，﹣0.82，﹣30
，3.14，﹣2，0，﹣2011，﹣3.1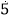
，
，﹣
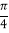，2.010010001…，正分数集合：{ …}
整数集合：{ …}
负有理数集合：{ …}
非正整数集合；{ …}
无理数集合：{ …}．
-
科目： 来源： 题型：
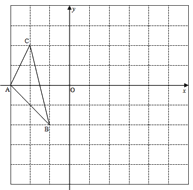
查看答案和解析>>【题目】如图，图中的小方格都是边长为1的正方形，△ABC的顶点坐标分别为：A（-3，0），B（-1，-2），C（-2，2）．
（1）请在图中画出△ABC绕B点顺时针旋转90°后的图形△A′BC′.
（2）请直接写出以A′、B、C′为顶点平行四边形的第4个顶点D的坐标.
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知二次函数y=x2+bx+c（b，c为常数）．
（1）当b=2，c=﹣3时，求二次函数图象的顶点坐标；
（2）当c=10时，若在函数值y=1的情况下，只有一个自变量x的值与其对应，求此时二次函数的解析式；
（3）当c=b2时，若在自变量x的值满足b≤x≤b+3的情况下，与其对应的函数值y的最小值为21，求此时二次函数的解析式．
相关试题
