搜索
【题目】为了解同学对体育活动的喜爱情况，某校设计了“你最喜欢的体育活动是哪一项(仅限一项)”的调查问卷.该校对本校学生进行随机抽样调查，以下是根据调查数据得到的统计图的一部分.请根据以上信息解答以下问题：
(1)该校对多少名学生进行了抽样调查？
(2)请补全图1并标上数据.
(3)若该校共有学生900人，请你估计该校最喜欢跳绳项目的学生约有多少人？
参考答案：
【答案】(1)50人；(2)见解析；(3)90人.
【解析】
（1）根据喜欢羽毛球的有10人，占总人数的20%，即可求得总人数；
（2）用总人数50减去其它各项的人数即可求得喜欢其它类型的人数，然后补全统计图；
（3）利用全校学生人数900乘以抽查中得到的最喜欢跳绳项目的所占的百分比即可求解．
解：（1）抽样调查的总人数是：10÷20%=50（人）；
（2）喜爱其它运动的人数是：50-10-5-20=15（人）．
补全后的统计图如下：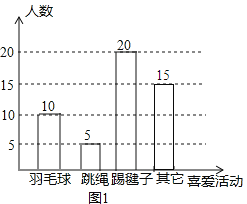
；
（3）该校最喜欢跳绳项目的学生约有900×10%=90（人）．
-
科目： 来源： 题型：
查看答案和解析>>【题目】阅读理解
如图1，已知点A是BC外一点，连接AB，AC，求∠BAC+∠B+∠C的度数．
（1）阅读并补充下面推理过程
解：过点A作ED∥BC
∴∠B=∠ ，∠C=∠ ．
又∵∠EAB+∠BAC+∠DAC=180°（平角定义）
∴∠B+∠BAC+∠C=180°
从上面的推理过程中，我们发现平行线具有“等角转化”的功能，将∠BAC，∠B，∠C“凑”在一起，得出角之间的关系，使问题得以解决
（2）如图2，已知AB∥ED，求∠B+∠BCD+∠D的度数．
小明受到启发，过点C作CF∥AB如图所示，请你帮助小明完成解答：
（3）已知AB∥CD，点C在点D的右侧，∠ADC=70°．BE平分∠ABC，DE平分∠ADC，BE，DE所在的直线交于点E，点E在AB与CD两条平行线之间．
①如图3，点B在点A的左侧，若∠ABC=60°，则∠BED的度数为 °．
②如图4，点B在点A的右侧，且AB＜CD，AD＜BC．若∠ABC=n°，则∠BED的度数为 °（用含n的代数式表示）
-
科目： 来源： 题型：
查看答案和解析>>【题目】满足下列条件的△ABC不是直角三角形的是（）
A. BC＝1，AC＝2，AB＝
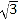
B. BC＝1，AC＝2，AB＝
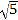
C. BC：AC：AB＝3：4：5
D. ∠A：∠B：∠C＝3：4：5
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知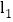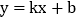直线
：
与直线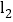
：
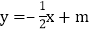都经过
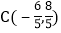，直线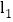交y轴于点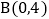
，交x轴于点A，直线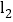交y轴于点D，P为y轴上任意一点，连接PA、PC，有以下说法：①方程组
的解为
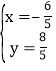；②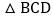
为直角三角形；③
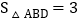；④当
的值最小时，点P的坐标为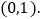
其中正确的说法个数有
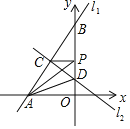
A. 1个B. 2个C. 3个D. 4个
-
科目： 来源： 题型：
查看答案和解析>>【题目】某社区准备在甲、乙两位射箭爱好者中选出一人参加集训，两人各射了5剑，他们的总成绩
单位：环
相同，小宇根据他们的成绩绘制了尚不完整的统计图表，并计算了甲成绩的平均数和方差见小宇的作业．
______，
______；
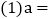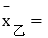请完成图中乙成绩变化情况的折线；
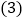观察你补全的折线图可以看出______填“甲”或“乙”的成绩比较稳定
参照小宇的计算方法，计算乙成绩的方差，并验证你的判断；并判断谁将被选中．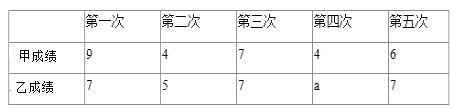
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在直角坐标系中，△ABC是格点三角形（三角形的三个顶点都是小正方形的顶点）．
（1）在第一象限内找一点P，以格点P、A、B为顶点的三角形与△ABC相似但不全等，请写出符合条件格点P的坐标；
（2）请用直尺与圆规在第一象限内找到两个点M、N，使∠AMB=∠ANB=∠ACB．请保留作图痕迹，不要求写画法．
-
科目： 来源： 题型：
查看答案和解析>>【题目】某超市销售有甲、乙两种商品，甲商品每件进价10元，售价15元；乙商品每件进价30元，售价40元.
(1)若该超市一次性购进两种商品共60件，且恰好用去1600元，问购进甲、乙两种商品各多少件？
(2)若该超市要使两种商品共60件的购进费用不超过1240元，且总利润(利润=售价-进价)不少于450元，请你帮助该超市设计相应的进货方案，并指出使该超市利润最大的方案.
相关试题
