【题目】为推进垃圾分类,推动绿色发展,某工厂购进甲、乙两种型号的机器人用来进行垃圾分类,甲型机器人比乙型机器人每小时多分20kg,甲型机器人分类800kg垃圾所用的时间与乙型机器人分类600kg垃圾所用的时间相等。
(1)两种机器人每小时分别分类多少垃圾?
(2)现在两种机器人共同分类700kg垃圾,工作2小时后甲型机器人因机器维修退出,求甲型机器人退出后乙型机器人还需工作多长时间才能完成?
参考答案:
【答案】(1)甲型机器人每小时分类80kg垃圾。则乙型机器人每小时分类60kg垃圾;(2)甲型机器人退出后乙型机器人还需要工作7小时
【解析】
(1)根据甲型机器人分类800kg垃圾所用的时间与乙型机器人分类600kg垃圾所用的时间相等列出方程求解即可;
(2)根据(1)求得的答案通过计算即可求得答案.
(1)解:设甲型机器人每小时分类![]() 垃圾。则乙型机器人每小时分类
垃圾。则乙型机器人每小时分类![]() 垃圾,
垃圾,
由题意得: ![]()
解得:![]()
检验:当![]() 时,
时,![]() ,
,
所以,原分式方程的解为![]() ,
,
![]()
答:甲型机器人每小时分类![]() 垃圾。则乙型机器人每小时分类
垃圾。则乙型机器人每小时分类![]() 垃圾;
垃圾;
(2)[700-(80+60)×2]÷60=7小时
答:甲型机器人退出后乙型机器人还需要工作7小时.
-
科目: 来源: 题型:
查看答案和解析>>【题目】问题背景:如图1,等腰△ABC中,AB=AC,∠BAC=120°,作AD⊥BC于点D,则D为BC的中点,∠BAD=
 ∠BAC=60°,于是
∠BAC=60°,于是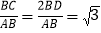 ;
;
迁移应用:如图2,△ABC和△ADE都是等腰三角形,∠BAC=∠DAE=120°,D,E,C三点在同一条直线上,连接BD.
(1)求证:△ADB≌△AEC;
(2)若AD=2,BD=3,请计算线段CD的长;
拓展延伸:如图3,在菱形ABCD中,∠ABC=120°,在∠ABC内作射线BM,作点C关于BM的对称点E,连接AE并延长交BM于点F,连接CE,CF.
(3)证明:△CEF是等边三角形;
(4)若AE=4,CE=1,求BF的长.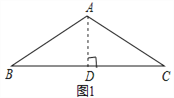


-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ ABC中,AB=AC,点D在线段BC上,AD=BD,△ ADC是等腰三角形,求△ABC三个内角的度数。

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,已知抛物线y=ax2+bx(a≠0)经过A(6,0)、B(8,8)两点.
(1)求抛物线的解析式;
(2)将直线OB向下平移m个单位长度后,得到的直线与抛物线只有一个公共点D,求m的值及点D的坐标;
(3)如图2,若点N在抛物线上,且∠NBO=∠ABO,则在(2)的条件下,在坐标平面内有点P,求出所有满足△POD∽△NOB的点P坐标(点P、O、D分别与点N、O、B对应).


-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△BAD和△BCE均为等腰直角三角形,∠BAD =∠BCE = 90°,点M为AN的中点,过点E与AD平行的直线交射线AM于点N。

(1)当A,B,C三点在同一直线上时(如图1),求证:AD=NE ;
(2)将图1中的△BCE绕点B旋转,当A,B,E三点在同一直线上时(如图2),求证:△ACN为等腰直角三角形;
(3)将图1中△BCE绕点B旋转到图3位置时,(2)中的结论是否仍成立?若成立,请证明;若不成立,请说明理由。
-
科目: 来源: 题型:
查看答案和解析>>【题目】自驾游是当今社会一种重要的旅游方式,五一放假期间小明一家人自驾去灵山游玩,下图描述了小明爸爸驾驶的汽车在一段时间内路程s(千米)与时间t(小时)的函数关系,下列说法中正确的是( )

A. 汽车在0~1小时的速度是60千米/时; B. 汽车在2~3小时的速度比0~0.5小时的速度快;
C. 汽车从0.5小时到1.5小时的速度是80千米/时; D. 汽车行驶的平均速度为60千米/时.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列5个结论:①abc<0;②b<a+c;③4a+2b+c>0;④2c<3b;⑤a+b<m(am+b)(m≠1且为实数),其中正确的个数是( )

A. 2个 B. 3个 C. 4个 D. 5个
相关试题

