【题目】解不等式,并把解集在数轴上表示出来:
(1)5x﹣6≤2(x+3);
(2)![]()
参考答案:
【答案】(1)x≤4; (2)x>﹣1,
【解析】【试题分析】(1)根据解一元一次不等式基本步骤:去括号、移项、合并同类项、系数化为1可得;
(2)根据解一元一次不等式基本步骤:去分母、去括号、移项、合并同类项、系数化为1可得.
【试题解析】(1)去括号,得:5x﹣6≤2x+6,
移项,得:5x﹣2x≤6+6,
合并同类项,得:3x≤12,
系数化为1,得:x≤4,
将解集表示在数轴上如下:
![]()
(2)去分母,得:2(2x﹣1)﹣(5x﹣1)<0,
去括号,得:4x﹣2﹣5x+1<0,
移项、合并,得:﹣x<1,
系数化为1,得:x>﹣1,
将解集表示在数轴上如下:
 .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,在长方形ABCD中,AB=DC=3cm,BC=5cm,点P从点B出发,以1 cm/s的速度沿BC向点C运动,设点P的运动时间为ts.
(1)PC= cm(用含t的代数式表示)
(2)当t为何值时,△ABP≌△DCP,请说明理由
(3)如图②,当点P从点B开始运动时,点Q从点C出发,以a cm/s的速度沿CD向点D运动,是否存在这样a的值,使得△ABP与△PCQ全等?若存在,请求出a的值,若不存在,请说明理由。

-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)若
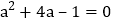 ,则
,则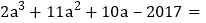
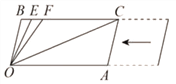
(2)如图,CB∥OA,∠B=∠A=108°,E、F在CB上,且满足∠FOC=∠AOC,OE平分∠BOF,若平行移动AC,当∠OCA= 时。可以使∠OEB=∠OCA。
-
科目: 来源: 题型:
查看答案和解析>>【题目】我们给出如下定义:顺次连接任意一个四边形各边中点所得的四边形叫中点四边形.

(1)如图1,四边形ABCD中,点E,F,G,H分别为边AB,BC,CD,DA的中点.求证:中点四边形EFGH是平行四边形;
(2)如图2,点P是四边形ABCD内一点,且满足PA=PB,PC=PD,∠APB=∠CPD,点E,F,G,H分别为边AB,BC,CD,DA的中点,猜想中点四边形EFGH的形状,并证明你的猜想;
(3)若改变(2)中的条件,使∠APB=∠CPD=90°,其他条件不变,直接写出中点四边形EFGH的形状.(不必证明)
-
科目: 来源: 题型:
查看答案和解析>>【题目】(10分)在东营市中小学标准化建设工程中,某学校计划购进一批电脑和电子白板,经过市场考察得知,购买1台电脑和2台电子白板需要3.5万元,购买2台电脑和1台电子白板需要2.5万元.
(1)求每台电脑、每台电子白板各多少万元?
(2)根据学校实际,需购进电脑和电子白板共30台,总费用不超过30万元,但不低于28万元,请你通过计算求出有几种购买方案,哪种方案费用最低.
-
科目: 来源: 题型:
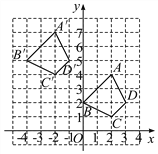
查看答案和解析>>【题目】四边形ABCD各顶点的坐标分别为A(2,4)、B(0,2)、C(2,1)、D(3,2),将四边形向左平移4个单位长度,再向上平移3个单位长度,得到四边形A′B′C′D′.
(1)四边形A′B′C′D′与四边形ABCD对应点的横坐标有什么关系?纵坐标呢?分别写出A′B′C′D′的坐标;
(2)如果将四边形A′B′C′D′看成是由四边形ABCD经过一次平移得到的,请指出这一平移的方向和距离.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知点 A(x,y),若 xy=0,那么点 A 在___________________.
相关试题

