【题目】如图①,在长方形ABCD中,AB=DC=3cm,BC=5cm,点P从点B出发,以1 cm/s的速度沿BC向点C运动,设点P的运动时间为ts.
(1)PC= cm(用含t的代数式表示)
(2)当t为何值时,△ABP≌△DCP,请说明理由
(3)如图②,当点P从点B开始运动时,点Q从点C出发,以a cm/s的速度沿CD向点D运动,是否存在这样a的值,使得△ABP与△PCQ全等?若存在,请求出a的值,若不存在,请说明理由。

参考答案:
【答案】(1)5t;(2)t=2.5 (3)a=1或a=1.2
【解析】分析: (1)根据题意求出BP,计算即可;
(2)根据全等三角形的判定定理解答;
(3)分△ABP≌△QCP和△ABP≌△PCQ两种情况,根据全等三角形的性质解答.
详解:
(1)∵点P的速度是1cm/s,
∴ts后BP=tcm,
∴PC=BCBP=(5t)cm,
(2)当t=2.5时,△ABP≌△DCP,
∵当t=2.5时,BP=CP=2.5,
在△ABP和△DCP中,
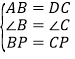
∴△ABP≌△DCP;
(3)∵∠B=∠C=90°,
∴当AB=PC,BP=CQ时,△ABP≌△PCQ,
∴5t=3,t=at,
解得,t=2,a=1,
当AB=QC,BP=CP时,△ABP≌△QCP,
此时,点P为BC的中点,点Q与点D重合,
∴t=2.5,at=3,
解得,a=1.2,
综上所述,当a=1或a=1.2时,△ABP与△PCQ全等。
点睛: 本题考查的是矩形的性质、全等三角形的判定和性质,掌握矩形的对边相等、四个角都是直角以及全等三角形的判定定理和性质定理、灵活运用分情况讨论思想是解题的关键.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在2017年十堰市初中体育中考中,随意抽取某校5位同学跳远的记录分别为:158,160,154,158,170,则由这组数据得到的结论错误的是( )
A.平均数为160
B.中位数为158
C.众数为158
D.方差为20.3 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知,点 M 在第四象限,它到 x 轴的距离为 6,到 y 轴的距离为 3,则点 M的坐标为________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在ABCD中,点E,F在对角线AC上,且AE=CF.求证:
(1)DE=BF;
(2)四边形DEBF是平行四边形.

-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)若
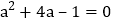 ,则
,则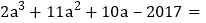
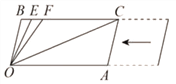
(2)如图,CB∥OA,∠B=∠A=108°,E、F在CB上,且满足∠FOC=∠AOC,OE平分∠BOF,若平行移动AC,当∠OCA= 时。可以使∠OEB=∠OCA。
-
科目: 来源: 题型:
查看答案和解析>>【题目】我们给出如下定义:顺次连接任意一个四边形各边中点所得的四边形叫中点四边形.

(1)如图1,四边形ABCD中,点E,F,G,H分别为边AB,BC,CD,DA的中点.求证:中点四边形EFGH是平行四边形;
(2)如图2,点P是四边形ABCD内一点,且满足PA=PB,PC=PD,∠APB=∠CPD,点E,F,G,H分别为边AB,BC,CD,DA的中点,猜想中点四边形EFGH的形状,并证明你的猜想;
(3)若改变(2)中的条件,使∠APB=∠CPD=90°,其他条件不变,直接写出中点四边形EFGH的形状.(不必证明)
-
科目: 来源: 题型:
查看答案和解析>>【题目】解不等式,并把解集在数轴上表示出来:
(1)5x﹣6≤2(x+3);
(2)

相关试题

