【题目】（1）若，则

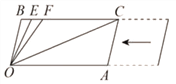
（2）如图，CB∥OA，∠B=∠A=108°，E、F在CB上，且满足∠FOC=∠AOC，OE平分∠BOF，若平行移动AC，当∠OCA= 时。可以使∠OEB=∠OCA。

参考答案：

【答案】（1）-2014 （2）54°

【解析】分析: （1）方程移项变形后，得：a2-4a=1，a2=4a+1，再将代数式中的a3化为2a2a=2a（4a+1），达到降次的目的，合并同类项后，最后提取公因式，代入可得结论；

（2）由于BC∥OA，∠B=108°，易求∠AOB，而OE、OC都是角平分线，从而可求∠COE；设∠OCA=α，∠AOC=x，根据三角形的外角性质、三角形的内角和定理、平行线的性质可得，α+x=72°，36°+x=α，解即可.

详解: ：（1）a2+4a-1=0，

移项得：a2+4a=1，a2=1-4a，

则2a3+11a2+10a-2017，

=2a（1-4a）+11a2+10a-2017，

=2a-8a+11a2+10a-2017，

=3a2+12a-2017，

=3（a2+4a）-2017，

=3×1-2017，

=-2014；

（2））∵CB∥OA，

∴∠BOA+∠B=180°，

∴∠BOA=180°-108°=72°，

∵∠FOC=∠AOC，OE平分∠BOF，

∴∠EOC=∠EOF+∠FOC=∠BOF+∠FOA=（∠BOF+∠FOA）=×72°=36°；

在平行移动AC的过程中，存在∠OEB=∠OCA，

设∠OCA=α，∠AOC=x，

∵∠OEB=∠COE+∠OCB=36°+x，

∠ACO=72°-x，

∴α=72°-x，36°+x=α，

72-x=36+x，

∴x=18°，α=54°．

即：当∠OCA=54度时．可以使∠OEB=∠OCA.

点睛: 本题考查了因式分解的应用、平行线的性质、角平分线的定义及平移的性质，两直线平行时，应该想到它们的性质，由两直线平行的关系得到角之间的数量关系，从而达到解决问题的目的.

关闭