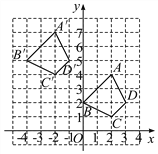
【题目】四边形ABCD各顶点的坐标分别为A(2,4)、B(0,2)、C(2,1)、D(3,2),将四边形向左平移4个单位长度,再向上平移3个单位长度,得到四边形A′B′C′D′.
(1)四边形A′B′C′D′与四边形ABCD对应点的横坐标有什么关系?纵坐标呢?分别写出A′B′C′D′的坐标;
(2)如果将四边形A′B′C′D′看成是由四边形ABCD经过一次平移得到的,请指出这一平移的方向和距离.
参考答案:
【答案】见解析.
【解析】试题分析: (1)根据图形,分别写出四边形A′B′C′D′与四边形ABCD各顶点坐标,对比发现:对应点的横坐标分别减了4,纵坐标分别加了3,A′(-2,7),B′(-4,5),C′(-2,4),D′(-1,5),
(2)连接AA′,根据勾股定理算出:AA′=![]() =5.如果将四边形A′B′C′D′看成是由四边形ABCD经过一次平移得到的,那么平移的方向是由A到A′的方向,平移的距离是5个单位长度.
=5.如果将四边形A′B′C′D′看成是由四边形ABCD经过一次平移得到的,那么平移的方向是由A到A′的方向,平移的距离是5个单位长度.
试题解析:(1)四边形A′B′C′D′与四边形ABCD相比,对应点的横坐标分别减了4,纵坐标分别加了3,A′(-2,7),B′(-4,5),C′(-2,4),D′(-1,5),
(2)连接AA′,则AA′=![]() =5.因此,如果将四边形A′B′C′D′看成是由四边形ABCD经过一次平移得到的,那么平移的方向是由A到A′的方向,平移的距离是5个单位长度.
=5.因此,如果将四边形A′B′C′D′看成是由四边形ABCD经过一次平移得到的,那么平移的方向是由A到A′的方向,平移的距离是5个单位长度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】我们给出如下定义:顺次连接任意一个四边形各边中点所得的四边形叫中点四边形.

(1)如图1,四边形ABCD中,点E,F,G,H分别为边AB,BC,CD,DA的中点.求证:中点四边形EFGH是平行四边形;
(2)如图2,点P是四边形ABCD内一点,且满足PA=PB,PC=PD,∠APB=∠CPD,点E,F,G,H分别为边AB,BC,CD,DA的中点,猜想中点四边形EFGH的形状,并证明你的猜想;
(3)若改变(2)中的条件,使∠APB=∠CPD=90°,其他条件不变,直接写出中点四边形EFGH的形状.(不必证明)
-
科目: 来源: 题型:
查看答案和解析>>【题目】解不等式,并把解集在数轴上表示出来:
(1)5x﹣6≤2(x+3);
(2)

-
科目: 来源: 题型:
查看答案和解析>>【题目】(10分)在东营市中小学标准化建设工程中,某学校计划购进一批电脑和电子白板,经过市场考察得知,购买1台电脑和2台电子白板需要3.5万元,购买2台电脑和1台电子白板需要2.5万元.
(1)求每台电脑、每台电子白板各多少万元?
(2)根据学校实际,需购进电脑和电子白板共30台,总费用不超过30万元,但不低于28万元,请你通过计算求出有几种购买方案,哪种方案费用最低.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知点 A(x,y),若 xy=0,那么点 A 在___________________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△A′B′C′是由△ABC平移后得到的,已知△ABC中一点P(x0,y0)经平移后对应点P′(x0+5,y0-2).
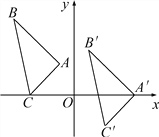
(1)已知A(-1,2),B(-4,5),C(-3,0),请写出A′、B′、C′的坐标;
(2)试说明△A′B′C′是如何由△ABC平移得到的;
(3)请直接写出△A′B′C′的面积为6.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列命题中正确的有( )
①如果|a|=|b|,那么a=b;
②两条直线被第三条直线所截,同位角相等;
③如果三条直线两两相交,那么可把一个平面最多分成6个部分;
④不是对顶角的角可以相等
A.1个B.2个C.3个D.4个
相关试题

