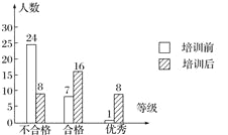
【题目】某校学生在电脑培训前后各参加了一次水平相同的考试,考分都以同一标准划分成“不合格”、“合格”、“优秀”三个等级.为了了解电脑培训的效果,随机抽取其中32名学生两次考试考分等级制成统计图(如图),试回答下列问题:
(1)这32名学生经过培训,考分等级“不合格”的百分比由________下降到________;
(2)估计该校640名学生,培训后考分等级为“合格”与“优秀”的学生共有多少名.
参考答案:
【答案】(1)75﹪,25﹪;(2)480名
【解析】
(1)用培训前后不合格的人数除以总人数即可得到培训前后的不合格率;
(2)求出培训后考分等级为合格与优秀的学生数,分别除以总人数乘以全校总人数即可.
解:(1)由条形统计图可知培训前不合格的由24人,培训后不合格的有8人,总人数为32人,
所以![]() ×100%=75%,
×100%=75%,![]() ×100%=25%.
×100%=25%.
所以培训前后不合格率分别为75%和25%,故答案为75%,25%.
(2)据题意,得培训后32名学生中“合格”与“优秀”的学生共有24名,
所以培训后全校考分等级为“合格”与“优秀”的学生人数约有640×![]() =480(名).
=480(名).
故答案为:(1)75%,25%.(2)480(名).
-
科目: 来源: 题型:
查看答案和解析>>【题目】把下列各数分别填入相应的集合中.
-
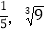 ,π,3.14,-
,π,3.14,-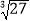 ,0,-5.123 45…,
,0,-5.123 45…,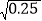 ,-
,- .
.(1)有理数集合:{ …};
(2)无理数集合:{ …};
(3)正实数集合:{ …};
(4)负实数集合:{ …}.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在Rt△ABC中,∠C=90°,Rt△ABC绕点A顺时针旋转到Rt△ADE的位置,点E在斜边AB上,连结BD,过点D作DF⊥AC于点F.
(1)如图1,若点F与点A重合,求证:AC=BC;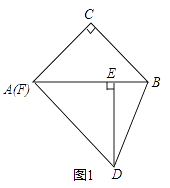
(2)若∠DAF=∠DBA,
①如图2,当点F在线段CA的延长线上时,判断线段AF与线段BE的数量关系,并说明理由;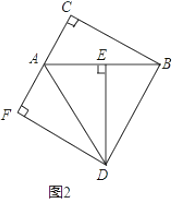
②当点F在线段CA上时,设BE=x,请用含x的代数式表示线段AF. -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面几何中,我们学过两条直线平行的定义,下面就两个一次函数的图象所确定的两条直线,给出它们平行的定义:设一次函数y=k1x+b1(k1≠0)的图象为直线l1,一次函数y=k2x+b2(k2≠0)的图象为直线l2,若k1=k2,且b1≠b2,我们就称直线l1与直线l2互相平行.解答下面的问题:
(1)求过点P(1,2),且与已知直线y=-2x-1平行的直线l的函数解析式,并画出图象;
(2)设直线l分别与y轴,x轴交于点A、B,如果直线m:y=kx+t(t>0)与直线l平行,且交x轴于点C,求出△ABC的面积S,关于t函数关系式.
-
科目: 来源: 题型:
查看答案和解析>>【题目】今年世界环境日(即6月5日),某市发布了一份空气质量的抽样调查报告,其中该市2~5月随机调查的25天各空气质量级别的天数如下表所示:

(1)试估计该市今年的空气质量主要是哪个级别?
(2)根据抽样数据,预测该市今年空气质量级别为优和良的天数共约为多少天?
(3)根据调查报告,试对有关部门提一条建设“绿色城市”的建议.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图一,抛物线y=ax2+bx+c与x轴正半轴交于A、B两点,与y轴交于点C,直线y=x﹣2经过A、C两点,且AB=2.
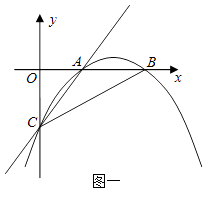
(1)求抛物线的解析式;
(2)若直线DE平行于x轴并从C点开始以每秒1个单位的速度沿y轴正方向平移,且分别交y轴、线段BC于点E,D,同时动点P从点B出发,沿BO方向以每秒2个单位速度运动,(如图2);当点P运动到原点O时,直线DE与点P都停止运动,连DP,若点P运动时间为t秒;设s=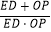 ,当t为何值时,s有最小值,并求出最小值.
,当t为何值时,s有最小值,并求出最小值.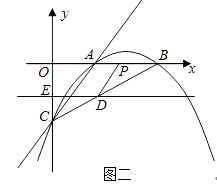
(3)在(2)的条件下,是否存在t的值,使以P、B、D为顶点的三角形与△ABC相似;若存在,求t的值;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】若点A(﹣1,2),B(2,﹣3)在直线y=kx+b上,则函数y=
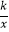 的图象在( )
的图象在( )
A.第一、三象限
B.第一、二象限
C.第二、四象限
D.第二、三象限
相关试题

