搜索
【题目】在平面直角坐标系中，
的斜边
在
轴上，点
的坐标为
，
，
，把先绕点顺时针旋转
，然后向下平移
个单位，则点
的对应点
的坐标为________．
参考答案：
【答案】
【解析】
根据直角三角形的性质和勾股定理可得BC，AB，利用直角三角形的面积可得AE，再利用射影定理易得BE，可得点A的坐标，根据旋转的性质易得D的坐标，再利用平移的性质可得结果．
作AE⊥BC，并作出把Rt△ABC先绕B点顺时针旋转180°后所得△DBC1，如图所示，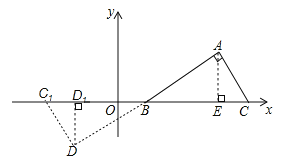
∵AC=2，∠ABC=30°，
∴BC=4
∴AB=2
，
∴AE＝
，
∴BE＝
，
∵点B坐标为（1，0），
∴A点的坐标为（4， ），
∵BE=3，
∴BD1=3，
∴D1坐标为（-2，0）
∴D坐标为（-2，-），
∵再向下平移2个单位，
∴D的坐标为（-2，-2-），
故答案是：（-2，-2-）．
-
科目： 来源： 题型：
查看答案和解析>>【题目】在平面直角坐标系xOy中（如图）．已知抛物线y=﹣
x2+bx+c经过点A（﹣1，0）和点B（0，
），顶点为C，点D在其对称轴上且位于点C下方，将线段DC绕点D按顺时针方向旋转90°，点C落在抛物线上的点P处．（1）求这条抛物线的表达式；
（2）求线段CD的长；
（3）将抛物线平移，使其顶点C移到原点O的位置，这时点P落在点E的位置，如果点M在y轴上，且以O、D、E、M为顶点的四边形面积为8，求点M的坐标．
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知：
，将
绕原点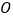
逆时针旋转
得到
，则点
的坐标是（ ）A. (-3,4) B. (-4,3) C. (3,-4) D. (4,-3)
-
科目： 来源： 题型：
查看答案和解析>>【题目】学校准备购进一批甲、乙两种办公桌若干张，并且每买1张办公桌必须买2把椅子，椅子每把100元，若学校购进20张甲种办公桌和15张乙种办公桌共花费24000元；购买10张甲种办公桌比购买5张乙种办公桌多花费2000元．
（1）求甲、乙两种办公桌每张各多少元？
（2）若学校购买甲乙两种办公桌共40张，且甲种办公桌数量不多于乙种办公桌数量的3倍，请你给出一种费用最少的方案，并求出该方案所需费用．
-
科目： 来源： 题型：
查看答案和解析>>【题目】把两个直角三角形如图
放置，使
与
重合，
与
相交于点
，其中
，
，
，
，
．图
中线段
的长
________
；
________
如图
，把
绕着点
逆时针旋转
度
得
，
与相交于点
，若
恰好是以
为底边的等腰三角形，求线段
的长．
-
科目： 来源： 题型：
查看答案和解析>>【题目】某高中学校为使高一新生入校后及时穿上合身的校服，现提前对某校九年级三班学生即将所穿校服型号情况进行了摸底调查，并根据调查结果绘制了如图两个不完整的统计图．（校服型号以身高作为标准，共分为6种型号）
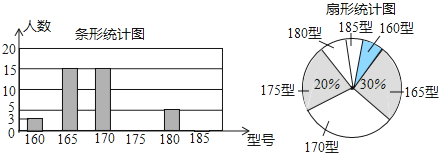
根据以上信息，解答下列问题：
（1）该班共有 名学生，其中穿175型校服的学生有 名；
（2）在条形统计图中，请把空缺部分补充完整；
（3）该班学生所穿校服型号的众数为 型，中位数为 型．
-
科目： 来源： 题型：
查看答案和解析>>【题目】．如图①，在△ABC 中，D、E 分别是 AB、AC 上的点，AB=AC，AD=AE，然后将△ADE 绕点 A 顺时针旋转一定角度，连接 BD，CE，得到图②，将 BD、CE 分别延长至 M、N，使 DM=
BD，EN=CE，得到图③，请解答下列问题：（1）在图②中，BD 与 CE 的数量关系是 ；
（2）在图③中，猜想 AM 与 AN 的数量关系，∠MAN 与∠BAC 的数量关系，并证明你的猜想．
相关试题
