【题目】如图,ABCD中,对角线AC,BD相交于O,BD=2AD,E,F,G分别是OC,OD,AB的中点,下列结论

①BE⊥AC
②四边形BEFG是平行四边形
③EG=GF
④EA平分∠GEF
其中正确的是( )
A. ①②③B. ①②④C. ①③④D. ②③④
参考答案:
【答案】B
【解析】
由平行四边形的性质可得OB=BC,由等腰三角形的性质可判断①正确,由直角三角形的性质和三角形中位线定理可判断③错误,由BG=EF,BG∥EF∥CD可证四边形BEFG是平行四边形,可得②正确.由平行线的性质和等腰三角形的性质可判断④正确.
∵四边形ABCD是平行四边形,
∴BO=DO=![]() BD,AD=BC,AB=CD,AB∥BC,
BD,AD=BC,AB=CD,AB∥BC,
又∵BD=2AD,
∴OB=BC=OD=DA,且点E 是OC中点,
∴BE⊥AC,
故①正确,
∵E、F分别是OC、OD的中点,
∴EF∥CD,EF=![]() CD,
CD,
∵点G是Rt△ABE斜边AB上的中点,
∴GE=![]() AB=AG=BG,
AB=AG=BG,
∴EG=EF=AG=BG,无法证明GE=GF,
故③错误,
∵BG=EF,BG∥EF∥CD,
∴四边形BEFG是平行四边形,
故②正确,
∵EF∥CD∥AB,
∴∠BAC=∠ACD=∠AEF,
∵AG=GE,
∴∠GAE=∠AEG,
∴∠AEG=∠AEF,
∴AE平分∠GEF,故④正确,
故选B.
-
科目: 来源: 题型:
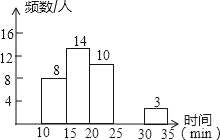
查看答案和解析>>【题目】某校中午学生用餐比较拥挤,为建议学校分年级错时用餐,李老师带领数学学习小组在某天随机调查了部分学生,统计了他们从下课到就餐结束所用的时间,并绘制成统计表和如图所示的不完整统计图.
根据以上提供的信息,解答下列问题:
(1)表中a=_____,b=_____,c=_____,补全频数分布直方图;
(2)此次调查中,中位数所在的时间段是_____min.
时间分段/min
频(人)数
百分比
10≤x<15
8
20%
15≤x<20
14
a
20≤x<25
10
25%
25≤x<30
b
12.50%
30≤x<35
3
7.50%
合计
c
100%
(3)这所学校共有1200人,试估算从下课到就餐结束所用时间不少于20min的共有多少人?
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲,乙两名选手参加长跑比赛,乙从起点出发匀速跑到终点,甲先快后慢,半个小时后找到适合自己的速度,匀速跑到终点,他们所跑的路程y(单位:km)随时间x(单位:h)变化的图象,如图所示,则下列结论错误的是( )
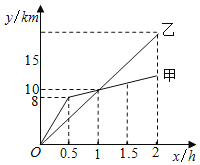
A. 在起跑后1h内,甲在乙的前面
B. 跑到1h时甲乙的路程都为10km
C. 甲在第1.5时的路程为11km
D. 乙在第2h时的路程为20km
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列变形中:
①由方程
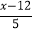 =2去分母,得x﹣12=10;
=2去分母,得x﹣12=10;②由方程
 x=
x= 两边同除以
两边同除以 ,得x=1;
,得x=1;③由方程6x﹣4=x+4移项,得7x=0;
④由方程2﹣
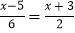 两边同乘以6,得12﹣x﹣5=3(x+3).
两边同乘以6,得12﹣x﹣5=3(x+3).错误变形的个数是( )个.
A. 4 B. 3 C. 2 D. 1
-
科目: 来源: 题型:
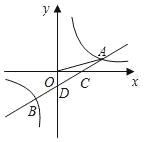
查看答案和解析>>【题目】如图,一次函数y=ax+b的图象与反比例函数y=
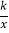 的图象交于A,B两点,与x轴交于点C,与y轴交于点D,已知OA=
的图象交于A,B两点,与x轴交于点C,与y轴交于点D,已知OA=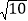 ,tan∠AOC=
,tan∠AOC= ,点B的坐标为(m,﹣2).
,点B的坐标为(m,﹣2).(1)求反比例函数的解析式;
(2)求一次函数的解析式.
-
科目: 来源: 题型:
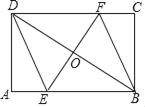
查看答案和解析>>【题目】如图,在矩形ABCD中,AB=8,BC=4,过对角线BD的中点O的直线分别交AB、CD于点E、F,连接DE,BF.
(1)求证:四边形BEDF是平行四边形;
(2)当四边形BEDF是菱形时,求EF的长.
-
科目: 来源: 题型:
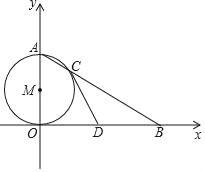
查看答案和解析>>【题目】如图,OA是⊙M的直径,点B在x轴上,连接AB交⊙M于点C.
(1)若点A的坐标为(0,2),∠ABO=30°,求点B的坐标.
(2)若D为OB的中点,求证:直线CD是⊙O的切线.
相关试题

