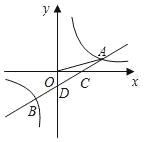
【题目】如图,一次函数y=ax+b的图象与反比例函数y=![]() 的图象交于A,B两点,与x轴交于点C,与y轴交于点D,已知OA=
的图象交于A,B两点,与x轴交于点C,与y轴交于点D,已知OA=![]() ,tan∠AOC=
,tan∠AOC=![]() ,点B的坐标为(m,﹣2).
,点B的坐标为(m,﹣2).
(1)求反比例函数的解析式;
(2)求一次函数的解析式.
参考答案:
【答案】(1)反比例函数的解析式是y=![]() ;(2)一次函数的解析式是y=
;(2)一次函数的解析式是y=![]() x﹣1.
x﹣1.
【解析】分析:(1)过A作AE⊥X轴于E,由tan∠AOE=![]() ,得到OE=3AE,根据勾股定理即可求出AE和OE的长,即得到A的坐标,代入双曲线即可求出k的值,得到解析式;
,得到OE=3AE,根据勾股定理即可求出AE和OE的长,即得到A的坐标,代入双曲线即可求出k的值,得到解析式;
(2)把B的坐标代入反比例函数的解析式即可求出B的坐标,把A和B的坐标代入一次函数的解析式即可求出a、b的值,即得到答案.
详解:(1)过A作AE⊥X轴于E,
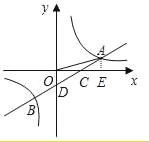
tan∠AOE=![]() ,
,
∴OE=3AE,
∵OA=![]() ,由勾股定理得:OE2+AE2=10,
,由勾股定理得:OE2+AE2=10,
解得:AE=1,OE=3,
∴A的坐标为(3,1),
A点在双曲线上,
∴1=![]() ,
,
∴k=3,
∴双曲线的解析式y=![]() .
.
答:反比例函数的解析式是y=![]() .
.
(2)解:B(m,﹣2)在双曲y=![]() 上,
上,
∴﹣2=![]() ,
,
解得:m=﹣![]() ,
,
∴B的坐标是(﹣![]() ,﹣2),
,﹣2),
代入一次函数的解析式得: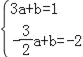 ,
,
解得:![]() ,
,
∴一次函数的解析式为:y=![]() x﹣1.
x﹣1.
答:一次函数的解析式是y=![]() x﹣1.
x﹣1.
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲,乙两名选手参加长跑比赛,乙从起点出发匀速跑到终点,甲先快后慢,半个小时后找到适合自己的速度,匀速跑到终点,他们所跑的路程y(单位:km)随时间x(单位:h)变化的图象,如图所示,则下列结论错误的是( )
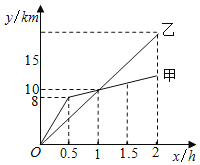
A. 在起跑后1h内,甲在乙的前面
B. 跑到1h时甲乙的路程都为10km
C. 甲在第1.5时的路程为11km
D. 乙在第2h时的路程为20km
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列变形中:
①由方程
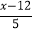 =2去分母,得x﹣12=10;
=2去分母,得x﹣12=10;②由方程
 x=
x= 两边同除以
两边同除以 ,得x=1;
,得x=1;③由方程6x﹣4=x+4移项,得7x=0;
④由方程2﹣
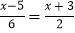 两边同乘以6,得12﹣x﹣5=3(x+3).
两边同乘以6,得12﹣x﹣5=3(x+3).错误变形的个数是( )个.
A. 4 B. 3 C. 2 D. 1
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,ABCD中,对角线AC,BD相交于O,BD=2AD,E,F,G分别是OC,OD,AB的中点,下列结论

①BE⊥AC
②四边形BEFG是平行四边形
③EG=GF
④EA平分∠GEF
其中正确的是( )
A. ①②③B. ①②④C. ①③④D. ②③④
-
科目: 来源: 题型:
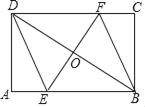
查看答案和解析>>【题目】如图,在矩形ABCD中,AB=8,BC=4,过对角线BD的中点O的直线分别交AB、CD于点E、F,连接DE,BF.
(1)求证:四边形BEDF是平行四边形;
(2)当四边形BEDF是菱形时,求EF的长.
-
科目: 来源: 题型:
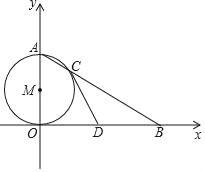
查看答案和解析>>【题目】如图,OA是⊙M的直径,点B在x轴上,连接AB交⊙M于点C.
(1)若点A的坐标为(0,2),∠ABO=30°,求点B的坐标.
(2)若D为OB的中点,求证:直线CD是⊙O的切线.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某汽车交易市场为了解二手轿车的交易情况,将本市场去年成交的二手轿车的全部数据,以二手轿车交易前的使用时间为标准分为A、B、C、D、E五类,并根据这些数据由甲,乙两人分别绘制了下面的两幅统计图(图都不完整).

请根据以上信息,解答下列问题:
(1)该汽车交易市场去年共交易二手轿车 辆.
(2)把这幅条形统计图补充完整.(画图后请标注相应的数据)
(3)在扇形统计图中,D类二手轿车交易辆数所对应扇形的圆心角为 度.
相关试题

