【题目】学校计划用地面砖铺设教学楼前矩形广场的地面ABCD已知矩形广场地面的长为100米,宽为80米.图案设计如图所示:广场的四角为小正方形,阴影部分为四个矩形,四个矩形的宽都为小正方形的边长,阴影部分铺绿色地面砖,其余部分铺白色地面砖.
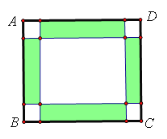
(1)要使铺白色地面砖的面积为5200平方米,则矩形广场四角的小正方形的边长为多少米?
(2)如果铺白色地面砖的费用为每平方米30元,铺绿色地面砖的费用为每平方米20元.当广场四角小正方形的边长为多少米时,铺广场地面的总费用最少?最少费用是多少?
参考答案:
【答案】(1) 10米或35米;(2)22.5,199500.
【解析】
试题分析:(1)设矩形广场四角的小正方形的边长为x米,根据等量关系“白色地板砖的面积=4个小正方形的面积+中间矩形的面积”列出一元二次方程求解即可;
(2)设铺矩形广场地面的总费用为y元,广场四角的小正方形的边长为x米,根据等量关系“总费用=铺白色地面砖的费用+铺绿色地面砖的费用”列出y关于x的函数,求得最小值.
试题解析:(1)设矩形广场四角的小正方形的边长为x米,根据题意,得:
4x2+(100﹣2x)(80﹣2x)=5200
整理,得:x2﹣45x+350=0(3分)
解之,得:x1=35,x2=10,
∴要使铺白色地面砖的面积为5200平方米,则矩形广场四角的小正方形的边长为10米或35米.
(2)设铺矩形广场地面的总费用为y元,广场四角的小正方形的边长为x米,则,
y=30×[4x2+(100﹣2x)(80﹣2x)]+20×[2x(100﹣2x)+2x(80﹣2x)]
即:y=80x2﹣3600x+240000
配方得,y=80(x﹣22.5)2+199500
当x=22.5时,y的值最小,最小值为199500.
∴当矩形广场四角的小正方形的边长为22.5米时,所铺广场地面的总费用最少,最少费用为199500元.
考点: 1.二次函数的应用;2.一元二次方程的应用.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,兰兰站在河岸上的G点,看见河里有一只小船沿垂直于岸边的方向划过来,此时,测得小船C的俯角是∠FDC=30°,若兰兰的眼睛与地面的距离是1.5米,BG=1米,BG平行于AC所在的直线,迎水坡的坡度i=4:3,坡长AB=10米,求小船C到岸边的距离CA的长?(参考数据:
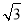 =1.73,结果保留两位有效数字)
=1.73,结果保留两位有效数字)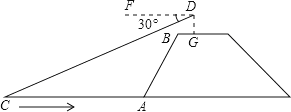
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)已知xm=2,xn=3,求x2m+3n的值;
(2)先化简,再求值:(a+2b)(a-2b)+(a+2b)2+(2ab2-8a2b2)÷2ab,其中a=1,b=2.
-
科目: 来源: 题型:
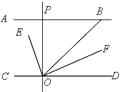
查看答案和解析>>【题目】如图,AB∥CD,OE平分∠BOC,OF⊥OE, OP⊥CD,∠ABO=40°,则下列结论:①∠BO E=70°;②OF平分∠BOD;③∠POE=∠BOF;④∠POB=2∠DOF.其中正确结论有(填序号)
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系xOy中,点P(-3,5)关于y轴的对称点的坐标是( )
A. (3,5) B. (3,-5) C. (5,-3) D. (-3,-5)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知:∠A=∠F,∠C=∠D,求证:BD∥EC,下面是不完整的说明过程,请将过程及其依据补充完整.
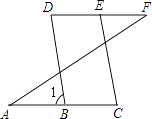
证明:∵∠A=∠F(已知)
∴AC∥()
∴∠D=∠1()
又∵∠C=∠D(已知)
∴∠1=()
∴BD∥CE() -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图所示,. l1∥l2,∠1+∠2=180°
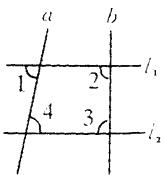
(1)求证:∠1=∠3.
(2)求∠2+∠4的度数.
相关试题

