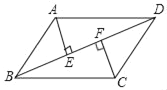
【题目】如图,平行四边形ABCD中,AE⊥BD于点E,CF⊥BD于点F,连结AF、CE.
(1)求证:四边形AECF是平行四边形;
(2)若AB=6,AD=2![]() ,∠ABD=30°,求四边形AECF的面积.
,∠ABD=30°,求四边形AECF的面积.
参考答案:
【答案】(1)证明见解析;(2)6![]() .
.
【解析】
(1)由四边形ABCD是平行四边形,可得AB=CD,AB∥CD,又由AE⊥BD,CF⊥BD,即可得AE∥CF,∠AEB=∠CFD=90°,然后利用AAS证得△AEB≌△CFD,即可得AE=CF,由有一组对边相等且平行的四边形是平行四边形,即可证得四边形AECF是平行四边形.
(2)根据直角三角形中30°的角所对的直角边为斜边的一半,求出AE和BE的长,再根据勾股定理求出DE的长,从而求出DF和EF的长,根据S平行四边形AECF=底![]() 高计算即可;
高计算即可;
(1)连接AF、EC.
∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD,
∴∠ABE=∠CDF,
∵AE⊥BD,CF⊥BD,
∴AE∥CF,∠AEB=∠CFD=90°,
在△AEB和△CFD中,
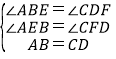 ,
,
∴△AEB≌△CFD(AAS),
∴AE=CF,
∴四边形AECF是平行四边形.
(2)在Rt△ABE中,∵AB=6,∠ABD=30°,
∴AE=![]() AB=3,BE=
AB=3,BE=![]() AE=3
AE=3![]() ,
,
在Rt△ADE中,AD=2![]() ,
,
DE=![]()
∵△AEB≌△CFD,
∴BE=DF=3![]() ,
,
∴EF=DE-DF=2![]() ,
,
∴S平行四边形AECF=![]() =6
=6![]() .
.

-
科目: 来源: 题型:
查看答案和解析>>【题目】我们知道对于一个图形,通过不同的方法计算图形的面积时,可以得到一个数学等式.例如由图1可以得到
 .请回答下列问题:
.请回答下列问题:
(1)写出图2中所表示的数学等式是 ;
(2)如图3,用四块完全相同的长方形拼成正方形,用不同的方法,计算图中阴影部分的面积,你能发现什么?(用含有
 ,
, 的式子表示) ;
的式子表示) ;(3)通过上述的等量关系,我们可知: 当两个正数的和一定时,它们的差的绝对值越小,则积越 (填“ 大”“或“小”);当两个正数的积一定时,它们的差的绝对值越小,则和越 (填“ 大”或“小”).
-
科目: 来源: 题型:
查看答案和解析>>【题目】不等式组
 的最大整数解为 .
的最大整数解为 . -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD的边长为6,分别以A、B为圆心,6为半径画
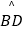 、
、 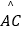 ,则图中阴影部分的面积为 .
,则图中阴影部分的面积为 . 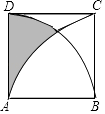
-
科目: 来源: 题型:
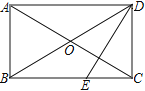
查看答案和解析>>【题目】如图,四边形ABCD中,对角线AC、BD相交于点O,AO=CO,BO=DO,且∠ABC+∠ADC=180°
(1) 求证:四边形ABCD是矩形
(2) 若DE⊥AC交BC于E,∠ADB∶∠CDB=2∶3,则∠BDE的度数是多少?
-
科目: 来源: 题型:
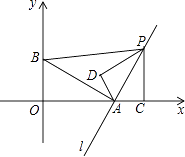
查看答案和解析>>【题目】如图,在直角坐标系中,点A(2,0),点B(0,1),过点A的直线l垂直于线段AB,点P是直线l上一动点,过点P作PC⊥x轴,垂足为C,把△ACP沿AP翻折180°,使点C落在点D处.若以A,D,P为顶点的三角形与△ABP相似,则所有满足此条件的点P的坐标为 .
-
科目: 来源: 题型:
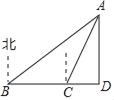
查看答案和解析>>【题目】如图,一艘轮船航行到B处时,测得小岛A在船的北偏东60°的方向上,轮船从B处继续向正东方向航行100海里到达C处时,测得小岛A在船的北偏东30°的方向上,AD⊥BC于点D,求AD的长.
相关试题

