【题目】如图,在△BCE中,点A是边BE上一点,以AB为直径的⊙O与CE相切于点D,AD∥OC,点F为OC与⊙O的交点,连接AF. 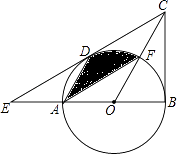
(1)求证:CB是⊙O的切线;
(2)若∠ECB=60°,AB=6,求图中阴影部分的面积.
参考答案:
【答案】
(1)证明:连接OD,与AF相交于点G,
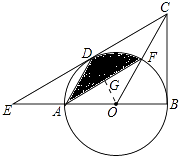
∵CE与⊙O相切于点D,
∴OD⊥CE,
∴∠CDO=90°,
∵AD∥OC,
∴∠ADO=∠DOC,∠DAO=∠BOC,
∵OA=OD,
∴∠ADO=∠DAO,
∴∠DOC=∠BOC,
在△CDO和△CBO中,
 ,
,
∴△CDO≌△CBO,
∴∠CBO=∠CDO=90°,
∴CB是⊙O的切线
(2)由(1)可知∠DOA=∠BCO,∠DOC=∠BOC,
∵∠ECB=60°,
∴∠DCO=∠BCO= ![]() ∠ECB=30°,
∠ECB=30°,
∴∠DOC=∠BOC=60°,
∴∠DOA=60°,
∵OA=OD,
∴△OAD是等边三角形,
∴AD=OD=OF,∵∠GOF=∠ADO,
在△ADG和△FOG中,
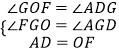 ,
,
∴△ADG≌△FOG,
∴S△ADG=S△FOG,
∵AB=6,
∴⊙O的半径r=3,
∴S阴=S扇形ODF= ![]() =
= ![]() π
π
【解析】(1)欲证明CB是⊙O的切线,只要证明BC⊥OB,可以证明△CDO≌△CBO解决问题.(2)首先证明S阴=S扇形ODF , 然后利用扇形面积公式计算即可.
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两个水桶中装有少量且重量相等的水,先把甲桶的水倒出三分之一给乙桶,再把乙桶的水倒出四分之一给甲桶(假设不会溢出),最后甲、乙两桶中水的重量的大小是( )
A. 甲桶中水的重量>乙桶中水的重量 B. 甲桶中水的重量=乙桶中水的重量
C. 甲桶中水的重量<乙桶中水的重量 D. 不能确定,与桶中原有水的重量有关
-
科目: 来源: 题型:
查看答案和解析>>【题目】将矩形OABC如图放置,O为原点.若点A(﹣1,2),点B的纵坐标是
 ,则点C的坐标是( )
,则点C的坐标是( )
A. (4,2) B. (2,4) C. (
 ,3) D. (3,
,3) D. (3, )
) -
科目: 来源: 题型:
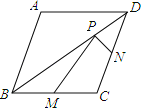
查看答案和解析>>【题目】已知菱形ABCD的两条对角线分别为6和8,M、N分别是边BC、CD的中点,P是对角线BD上一点,则PM+PN的最小值= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知点A、B在数轴上表示的数分别为m、n.
(1)对照数轴完成下表:

(2)若A、B两点间的距离为d,试写出d与m、n之间数量关系,并用文字语言描述
这个数量关系;
(3)已知A、B两点在数轴上表示的数分别为x和-2,则A、B两点的距离d可表示
为 ;如果d=3,求x的值。
(4)若数轴上表示数m的点位于表示数-5和3的点之间,求|m+5|+|m-3|的值(用含x的式子表示);
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图A在数轴上所对应的数为﹣2.
(1)点B在点A右边距A点4个单位长度,求点B所对应的数;
(2)在(1)的条件下,点A以每秒2个单位长度沿数轴向左运动,点 B 以每秒2个单位长度沿数轴向右运动,当点A运动到﹣6所在的点处时,求A,B两点间距离.
(3)在(2)的条件下,现A点静止不动,B点再以每秒2个单位长度沿数轴向左运动时,经过多长时间A,B两点相距4个单位长度.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,反比例函数y=
 的图象与一次函数y=kx+b的图象交于A,B两点,点A的坐标为(2,6),点B的坐标为(n,1).
的图象与一次函数y=kx+b的图象交于A,B两点,点A的坐标为(2,6),点B的坐标为(n,1). 
(1)求反比例函数与一次函数的表达式;
(2)点E为y轴上一个动点,若S△AEB=10,求点E的坐标.
相关试题

