【题目】如图,反比例函数y= ![]() 的图象与一次函数y=kx+b的图象交于A,B两点,点A的坐标为(2,6),点B的坐标为(n,1).
的图象与一次函数y=kx+b的图象交于A,B两点,点A的坐标为(2,6),点B的坐标为(n,1). 
(1)求反比例函数与一次函数的表达式;
(2)点E为y轴上一个动点,若S△AEB=10,求点E的坐标.
参考答案:
【答案】
(1)解:把点A(2,6)代入y= ![]() ,得m=12,
,得m=12,
则y= ![]() .
.
把点B(n,1)代入y= ![]() ,得n=12,
,得n=12,
则点B的坐标为(12,1).
由直线y=kx+b过点A(2,6),点B(12,1)得
![]() ,
,
解得 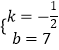 ,
,
则所求一次函数的表达式为y=﹣ ![]() x+7
x+7
(2)解:如图,直线AB与y轴的交点为P,设点E的坐标为(0,m),连接AE,BE,
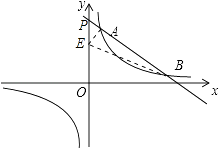
则点P的坐标为(0,7).
∴PE=|m﹣7|.
∵S△AEB=S△BEP﹣S△AEP=10,
∴ ![]() ×|m﹣7|×(12﹣2)=10.
×|m﹣7|×(12﹣2)=10.
∴|m﹣7|=2.
∴m1=5,m2=9.
∴点E的坐标为(0,5)或(0,9).
【解析】(1)把点A的坐标代入反比例函数解析式,求出反比例函数的解析式,把点B的坐标代入已求出的反比例函数解析式,得出n的值,得出点B的坐标,再把A、B的坐标代入直线y=kx+b,求出k、b的值,从而得出一次函数的解析式;(2)设点E的坐标为(0,m),连接AE,BE,先求出点P的坐标(0,7),得出PE=|m﹣7|,根据S△AEB=S△BEP﹣S△AEP=10,求出m的值,从而得出点E的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△BCE中,点A是边BE上一点,以AB为直径的⊙O与CE相切于点D,AD∥OC,点F为OC与⊙O的交点,连接AF.
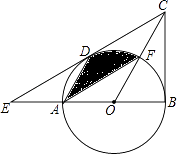
(1)求证:CB是⊙O的切线;
(2)若∠ECB=60°,AB=6,求图中阴影部分的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知点A、B在数轴上表示的数分别为m、n.
(1)对照数轴完成下表:

(2)若A、B两点间的距离为d,试写出d与m、n之间数量关系,并用文字语言描述
这个数量关系;
(3)已知A、B两点在数轴上表示的数分别为x和-2,则A、B两点的距离d可表示
为 ;如果d=3,求x的值。
(4)若数轴上表示数m的点位于表示数-5和3的点之间,求|m+5|+|m-3|的值(用含x的式子表示);
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图A在数轴上所对应的数为﹣2.
(1)点B在点A右边距A点4个单位长度,求点B所对应的数;
(2)在(1)的条件下,点A以每秒2个单位长度沿数轴向左运动,点 B 以每秒2个单位长度沿数轴向右运动,当点A运动到﹣6所在的点处时,求A,B两点间距离.
(3)在(2)的条件下,现A点静止不动,B点再以每秒2个单位长度沿数轴向左运动时,经过多长时间A,B两点相距4个单位长度.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正方形ABCD中,AD=
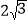 ,把边BC绕点B逆时针旋转30°得到线段BP,连接AP并延长交CD于点E,连接PC,则三角形PCE的面积为____________.
,把边BC绕点B逆时针旋转30°得到线段BP,连接AP并延长交CD于点E,连接PC,则三角形PCE的面积为____________.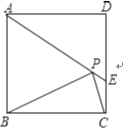
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将平行四边形
 沿
沿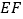 对折,使点
对折,使点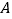 落在点
落在点 处,若
处,若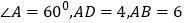 ,则
,则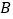 到
到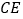 的距离为____________.
的距离为____________. 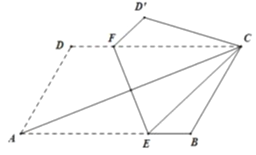
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知数轴上两点A、B对应的数分别为-1、3, 点P是数轴上一动点P

(1)(4分)若点P到点A,点B的距离相等,求点P对应的数;
(2) (6分)当点P以每分钟5个单位长度的速度从O点向右运动时,点A以每分钟3个单位长度的速度向右运动,点B以每分钟2个单位长度的速度向右运动,问几分钟时点P到点A,点B的距离相等.
相关试题

