搜索
【题目】某三角形中一个内角为80°，第二个内角为x°，第三个内角为y°，则y与x之间的关系式为________________．
参考答案：
【答案】y=-x+100
【解析】
由三角形内角和定理可求得答案．
解：由三角形内角和为180°可得：x+y+80=180，
∴y=-x+100，
故答案为：y=-x+100．
-
科目： 来源： 题型：
查看答案和解析>>【题目】为弘扬中华民族传统美德，增强少先队员的服务意识和奉献意识，2017年3月5日全国第54个“学雷锋日”暨第18个“中国青年志愿者服务日”之际，某校倡导学生们参加“学雷锋”义务劳动. 王校长为了解同学们的劳动情况（全体学生的劳动时间都大于0.5小时），随机调查了若干名学生某天内义务劳动的时间，并根据调查的数据绘制成如图1所示的不完整的频数分布直方图（注：0.5~1小时不包括0.5小时，包括1小时）和如图2所示的扇形统计图，已知劳动时间在0.5~1小时的学生人数比劳动时间在1~1.5小时的学生人数少2.
图1 图2
（1）求频数分布直方图中a，b的值；
（2）补全频数分布直方图；
（3）求劳动时间在2~2.5小时内的学生人数所对的扇形的圆心角的度数；
（4）若该校有1000名学生，义务劳动2小时以上的学生会获得学校的奖品，请你估计该校
有多少名学生获得了奖品？
-
科目： 来源： 题型：
查看答案和解析>>【题目】一个等腰三角形的两边长分别为5和2，则这个三角形的周长为_____．
-
科目： 来源： 题型：
查看答案和解析>>【题目】【问题提出】
学习了三角形全等的判定方法（即“SSS”、“ASA”、“AAS”、“SSS”）和直角三角形全等的判定方法（即“HL”）后，我们继续对“两个三角形满足两边和其中一边的对角对应相等”的情形进行研究．
【初步思考】
我们不妨将问题用符号语言表示为：在△ABC和△DEF中，AC=DF，BC=EF，∠B=∠E，然后，对∠B进行分类，可分为“∠B是直角、钝角、锐角”三种情况进行探究．
【深入探究】
第一种情况：当∠B是直角时，△ABC≌△DEF．
如图①，在△ABC和△DEF，AC=DF，BC=EF，∠B=∠E=90°，根据 ，可以知道Rt△ABC≌Rt△DEF．
第二种情况：当∠B是钝角时，△ABC≌△DEF．
如图②，在△ABC和△DEF，AC=DF，BC=EF，∠B=∠E，且∠B，∠E都是钝角，请你证明：△ABC≌△DEF（提示：过点C作CG⊥AB交AB的延长线于G，过点F作FH⊥DE交DE的延长线于H）．
第三种情况：当∠B是锐角时，△ABC和△DEF不一定全等．
在△ABC和△DEF，AC=DF，BC=EF，∠B=∠E，且∠B，∠E都是锐角，请你利用图③，在图③中用尺规作出△DEF，使△DEF和△ABC不全等．
-
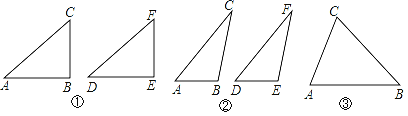
科目： 来源： 题型：
查看答案和解析>>【题目】已知A、B两地相距900 m，甲、乙两人同时从A地出发，以相同速度匀速步行，20 min后到达B地，甲随后马上沿原路按原速返回，回到A地后在原地等候乙回来；乙则在B地停留10 min后也沿原路以原速返回A地，则甲、乙两人之间的距离s（m）与步行时间t（min）之间的函数关系可以用图象表示为 （ ）
A.
B. 
C.
D. 
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知关于
的一元二次方程x2+2x+3k-6=0有两个不相等的实数根（1）求实数
的取值范围；（2）若
为正整数，且该方程的根都是整数，求
的值． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在长方形ABCD中，M是CD中点，AB=8，AD=3．
（1）求AM的长；
（2）△MAB是直角三角形吗？为什么？
相关试题
