[题目]已知关于的一元二次方程x2+2x+3k-6=0有两个不相等的实数根(1)求实数的取值范围,(2)若为正整数.且该方程的根都是整数.求的值．题目和参考答案 ——青夏教育精英家教网—

【题目】已知关于的一元二次方程x2+2x+3k-6=0有两个不相等的实数根

（1）求实数的取值范围；

（2）若为正整数，且该方程的根都是整数，求的值．

参考答案：

【答案】（1）；（2）1，2 .

【解析】

试题分析：（1）根据方程有两个不相等的实数根，得到根的判别式的值大于0列出关于k的不等式，求出不等式的解集即可得到k的范围.

（2）找出k范围中的整数解确定出k的值，经检验即可得到满足题意k的值．

试题解析：(1)由题意，得 Δ=4-4(3k-6)>0 ，

∴.

(2)∵k为正整数，∴k=1，2 .

当k=1时，方程x2+2x-3=0的根x1=-3，x2=1都是整数;

当k=2时，方程x2+2x=0的根x1=-2，x2=0都是整数.

综上所述，k=1，2.

相关试题

科目： 来源： 题型：

【题目】【问题提出】
学习了三角形全等的判定方法（即“SSS”、“ASA”、“AAS”、“SSS”）和直角三角形全等的判定方法（即“HL”）后，我们继续对“两个三角形满足两边和其中一边的对角对应相等”的情形进行研究．
【初步思考】
我们不妨将问题用符号语言表示为：在△ABC和△DEF中，AC=DF，BC=EF，∠B=∠E，然后，对∠B进行分类，可分为“∠B是直角、钝角、锐角”三种情况进行探究．
【深入探究】
第一种情况：当∠B是直角时，△ABC≌△DEF．
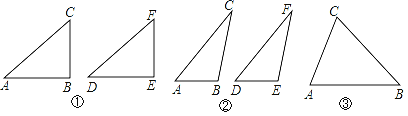
如图①，在△ABC和△DEF，AC=DF，BC=EF，∠B=∠E=90°，根据　　，可以知道Rt△ABC≌Rt△DEF．
第二种情况：当∠B是钝角时，△ABC≌△DEF．
如图②，在△ABC和△DEF，AC=DF，BC=EF，∠B=∠E，且∠B，∠E都是钝角，请你证明：△ABC≌△DEF（提示：过点C作CG⊥AB交AB的延长线于G，过点F作FH⊥DE交DE的延长线于H）．
第三种情况：当∠B是锐角时，△ABC和△DEF不一定全等．
在△ABC和△DEF，AC=DF，BC=EF，∠B=∠E，且∠B，∠E都是锐角，请你利用图③，在图③中用尺规作出△DEF，使△DEF和△ABC不全等．
查看答案和解析>>
科目： 来源： 题型：

【题目】某三角形中一个内角为80°，第二个内角为x°，第三个内角为y°，则y与x之间的关系式为________________．
查看答案和解析>>
科目： 来源： 题型：

【题目】已知A、B两地相距900 m，甲、乙两人同时从A地出发，以相同速度匀速步行，20 min后到达B地，甲随后马上沿原路按原速返回，回到A地后在原地等候乙回来；乙则在B地停留10 min后也沿原路以原速返回A地，则甲、乙两人之间的距离s（m）与步行时间t（min）之间的函数关系可以用图象表示为（　　）
A. B.
C. D.
查看答案和解析>>
科目： 来源： 题型：

【题目】如图，在长方形ABCD中，M是CD中点，AB=8，AD=3．
（1）求AM的长；
（2）△MAB是直角三角形吗？为什么？
查看答案和解析>>
科目： 来源： 题型：

【题目】一次函数的图像经过点（2，2）和（-1，8）．试求：
（1）这个函数的表达式；
（2）当 ﹣1＜x＜1时，求 y 的取值范围．
查看答案和解析>>
科目： 来源： 题型：

【题目】为了加强公民的节水意识，合理利用水资源，某城市规定用水收费标准如下：每户每月用水不超过6m3，水费按1.6元/m3收费；每户每月用水超过6m3时，超过的部分按4元/m3收费．设每户每月用水量为x（m3），应缴水费为y元．
（1）写出每月用水不超过6m3和超过6m3时，y与x之间的函数关系式．
（2）已知某户5月份的用水量为8m3，求该用户5月份的水费．
查看答案和解析>>