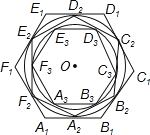
【题目】如图,正六边形A1B1C1D1E1F1的边长为2,正六边形A2B2C2D2E2F2的外接圆与正六边形A1B1C1D1E1F1的各边相切,正六边形A3B3C3D3E3F3的外接圆与正六边形A2B2C2D2E2F2的各边相切,…按这样的规律进行下去,A10B10C10D10E10F10的边长为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
参考答案:
【答案】D
【解析】
试题分析:连结OE1,OD1,OD2,如图,根据正六边形的性质得∠E1OD1=60°,则△E1OD1为等边三角形,再根据切线的性质得OD2⊥E1D1,于是可得OD2=![]() E1D1=
E1D1=![]() ×2,利用正六边形的边长等于它的半径得到正六边形A2B2C2D2E2F2的边长=
×2,利用正六边形的边长等于它的半径得到正六边形A2B2C2D2E2F2的边长=![]() ×2,同理可得正六边形A3B3C3D3E3F3的边长=(
×2,同理可得正六边形A3B3C3D3E3F3的边长=(![]() )2×2,依此规律可得正六边形A10B10C10D10E10F10的边长=(
)2×2,依此规律可得正六边形A10B10C10D10E10F10的边长=(![]() )9×2,然后化简即可
)9×2,然后化简即可
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,是小王和小李在一次跑步比赛中的时间和路程图.
(1)这次比赛的路程是_______米;
(2)小王的平均速度是_________米/秒;
(3)他们先到达终点的是_______;
(4)小李跑步的路程
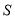 (米)与时间
(米)与时间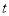 (秒)的函数关系式是_________.
(秒)的函数关系式是_________.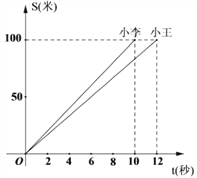
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数y=ax2-5x+c的图象如图所示,请根据图象回答下列问题:
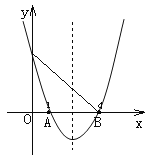
(1) a=_______,c=______.
(2)函数图象的对称轴是_________,顶点坐标P__________.
(3)该函数有最______值,当x=______时,y最值=________.
(4)当x_____时,y随x的增大而减小.当x_____时,y随x的增大而增大.
(5)抛物线与x轴交点坐标A_______,B________;与y轴交点C 的坐标为_______;
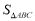 =_________,
=_________,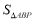 =________.
=________.(6)当y>0时,x的取值范围是_________;当y<0时,x的取值范围是_________.
(7)方程ax2-5x+c=0中△的符号为________.方程ax2-5x+c=0的两根分别为_____,____.
(8)当x=6时,y______0;当x=-2时,y______0.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知:
 平分
平分 ,
,  垂直平分
垂直平分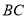 ,
,  ,
, 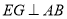 ,垂足分别是点
,垂足分别是点 、
、 .求证(1)
.求证(1)  ;(2)
;(2)  .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】王老师家买了一套新房,其结构如图所示(单位:m).他打算将卧室铺上木地板,其余部分铺上地砖.
(1)木地板和地砖分别需要多少平方米?
(2)如果地砖的价格为每平方米x元,木地板的价格为每平方米3x元,那么王老师需要花多少钱?

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正比例函数
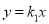 (
(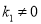 )的图像与反比例函数
)的图像与反比例函数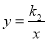 (
(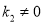 )的图像交于点
)的图像交于点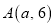 ,且点
,且点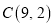 在反比例函数的图像上,点
在反比例函数的图像上,点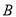 的坐标为
的坐标为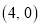 .
.(1)求正比例函数
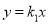 的解析式;
的解析式;(2)若
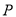 为射线
为射线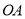 上一点,①若点
上一点,①若点 的横坐标为
的横坐标为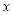 ,
, 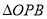 的面积为
的面积为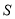 ,写出
,写出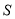 关于
关于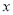 的函数解析式,并指出自变量
的函数解析式,并指出自变量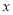 的取值范围;②当
的取值范围;②当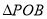 是等腰三角形时,求点
是等腰三角形时,求点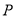 的坐标.
的坐标.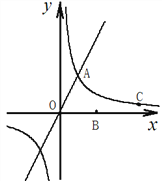
-
科目: 来源: 题型:
查看答案和解析>>【题目】我国出租车的收费标准因地而异,济宁市规定:起步价为6元,3千米之后每千米1.4元;济南市规定:起步价8元,3千米之后每千米1.2元.
(1)求济宁的李先生乘出租车2千米,5千米应付的车费;
(2)写出在济宁乘出租车行x千米时应付的车费;
(3)当行驶路程超过3千米,不超过l3千米时,求在济南、济宁两地坐出租车的车费相差多少?
(4)如果李先生在济南和济宁乘出租车所付的车费相等,试估算出李先生乘出租车多少千米(直接写出答案,不必写过程).
相关试题

