【题目】如图是一块地,已知AD=4m,CD=3m,AB=13m,BC=12m,且CD⊥AD,求这块地的面积. 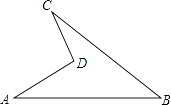
参考答案:
【答案】解:连接AC, 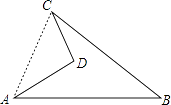
∵CD⊥AD
∴∠ADC=90°,
∵AD=4,CD=3,
∴AC2=AD2+CD2=42+32=25,
又∵AC>0,
∴AC=5,
又∵BC=12,AB=13,
∴AC2+BC2=52+122=169,
又∵AB2=169,
∴AC2+BC2=AB2 ,
∴∠ACB=90°,
∴S四边形ABCD=S△ABC﹣S△ADC=30﹣6=24m2 .
【解析】连接AC,利用勾股定理可以得出三角形ACD和ABC是直角三角形,△ABC的面积减去△ACD的面积就是所求的面积.
【考点精析】通过灵活运用勾股定理的概念和勾股定理的逆定理,掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2;如果三角形的三边长a、b、c有下面关系:a2+b2=c2,那么这个三角形是直角三角形即可以解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】16的算术平方根和25平方根的和是( )
A. 9 B. -1 C. 9或-1 D. -9或1
-
科目: 来源: 题型:
查看答案和解析>>【题目】陈老师给42名学生每人买了一件纪念品,其中有:每支12元的钢笔,每把4元的圆规,每册16元的词典,共用了216元,则陈老师买了钢笔支,词典册;
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在梯形ABCD中,AD∥BC,AB∥DE,AF∥DC,E、F两点在边BC上,且四边形AEFD是平行四边形.
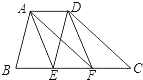
(1)AD与BC有何等量关系,请说明理由;
(2)当AB=DC时,求证:平行四边形AEFD是矩形. -
科目: 来源: 题型:
查看答案和解析>>【题目】某校开展了“互助、平等、感恩、和谐、进取”主题班会活动,活动后,就活动的5个主题进行了抽样调查(每位同学只选最关注的一个),根据调查结果绘制了两幅不完整的统计图.根据图中提供的信息,解答下列问题:

(1)这次调查的学生共有多少名?
(2)请将条形统计图补充完整,并在扇形统计图中计算出“进取”所对应的圆心角的度数.
(3)如果要在这5个主题中任选两个进行调查,根据(2)中调查结果,用树状图或列表法,求恰好选到学生关注最多的两个主题的概率(将互助、平等、感恩、和谐、进取依次记为A、B、C、D、E).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AD是∠BAC的平分线,DE∥AC交AB于E,DF∥AB交AC于F,求证:四边形AEDF是菱形.
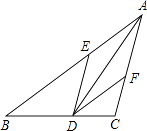
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,△ABC在平面直角坐标系中的位置如图①所示,A点坐标为(﹣4,0),B点坐标为(6,0),点D为BC的中点,点E为线段AB上一动点,连接DE经过点A、B、C三点的抛物线的解析式为
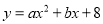 .
.(1)求抛物线的解析式;
(2)如图①,将△ADE以DE为轴翻折,点A的对称点为点G,当点G恰好落在抛物线的对称轴上时,求G点的坐标;
(3)如图②,当点E在线段AB上运动时,抛物线
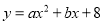 的对称轴上是否存在点F,使得以C、D、E、F为顶点的四边形为平行四边形?若存在,请直接写出点E、F的坐标;若不存在,请说明理由.
的对称轴上是否存在点F,使得以C、D、E、F为顶点的四边形为平行四边形?若存在,请直接写出点E、F的坐标;若不存在,请说明理由.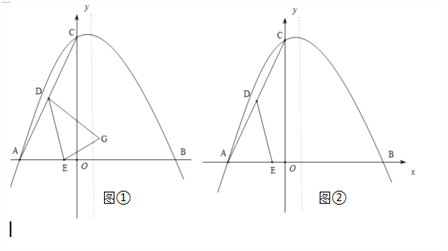
相关试题

