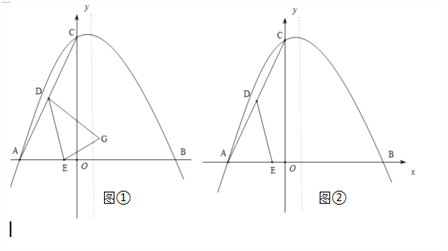
【题目】已知,△ABC在平面直角坐标系中的位置如图①所示,A点坐标为(﹣4,0),B点坐标为(6,0),点D为BC的中点,点E为线段AB上一动点,连接DE经过点A、B、C三点的抛物线的解析式为![]() .
.
(1)求抛物线的解析式;
(2)如图①,将△ADE以DE为轴翻折,点A的对称点为点G,当点G恰好落在抛物线的对称轴上时,求G点的坐标;
(3)如图②,当点E在线段AB上运动时,抛物线![]() 的对称轴上是否存在点F,使得以C、D、E、F为顶点的四边形为平行四边形?若存在,请直接写出点E、F的坐标;若不存在,请说明理由.
的对称轴上是否存在点F,使得以C、D、E、F为顶点的四边形为平行四边形?若存在,请直接写出点E、F的坐标;若不存在,请说明理由.
参考答案:
【答案】(1)![]() ;(2)(﹣1,
;(2)(﹣1, ![]() )或(﹣1,
)或(﹣1, ![]() );(3)F(﹣1,4)或(﹣1,﹣4)或(﹣1,12).
);(3)F(﹣1,4)或(﹣1,﹣4)或(﹣1,12).
【解析】试题分析:(1)把点A,B的坐标代入抛物线解析式,解方程组即可.
(2)作DM⊥抛物线的对称轴于点M,设G点的坐标为(﹣1,n),由翻折的性质,得到BD=DG;然后求出点D、点M的坐标,以及BC、BD的值;在Rt△GDM中,由勾股定理,求出n的值,即可求出G点的坐标.
(3)分三种情况讨论:①当CD∥EF,且点E在x轴的正半轴时;②当CD∥EF,且点E在x轴的负半轴时;③当CE∥DF时;然后根据平行四边形的性质,求出点F的坐标各是多少即可.
试题解析:(1)∵抛物线![]() 经过点A(﹣6,0),B(4,0),∴
经过点A(﹣6,0),B(4,0),∴![]() ,解得
,解得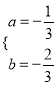 ,∴抛物线的解析式是:
,∴抛物线的解析式是: ![]() ;
;
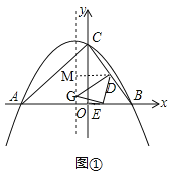
(2)如图①,作DM⊥抛物线的对称轴于点M,
 ,
,
设G点的坐标为(﹣1,n),由翻折的性质,可得BD=DG,∵B(4,0),C(0,8),点D为BC的中点,∴点D的坐标是(2,4),∴点M的坐标是(﹣1,4),DM=2﹣(﹣1)=3,∵B(4,0),C(0,8),∴BC=![]() =
=![]() ,∴BD=
,∴BD=![]() ,在Rt△GDM中,32+(4﹣n)2=20,解得n=
,在Rt△GDM中,32+(4﹣n)2=20,解得n=![]() ,∴G点的坐标为(﹣1,
,∴G点的坐标为(﹣1, ![]() )或(﹣1,
)或(﹣1, ![]() );
);
(3)抛物线![]() 的对称轴上存在点F,使得以C、D、E、F为顶点的四边形为平行四边形.
的对称轴上存在点F,使得以C、D、E、F为顶点的四边形为平行四边形.
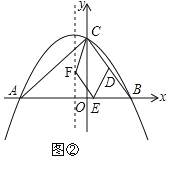
①当CD∥EF,且点E在x轴的正半轴时,如图②,
 ,
,
由(2),可得点D的坐标是(2,4),设点E的坐标是(c,0),点F的坐标是(﹣1,d),则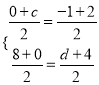 ,解得
,解得![]() ,∴点F的坐标是(﹣1,4),点C的坐标是(1,0);
,∴点F的坐标是(﹣1,4),点C的坐标是(1,0);
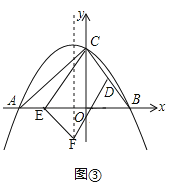
②当CD∥EF,且点E在x轴的负半轴时,如图③,
 ,
,
由(2),可得点D的坐标是(2,4),设点E的坐标是(c,0),点F的坐标是(﹣1,d),则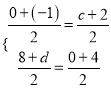 ,解得
,解得![]() ,∴点F的坐标是(﹣1,﹣4),点C的坐标是(﹣3,0);
,∴点F的坐标是(﹣1,﹣4),点C的坐标是(﹣3,0);
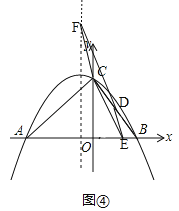
③当CE∥DF时,如图④,
 ,
,
由(2),可得点D的坐标是(2,4),设点E的坐标是(c,0),点F的坐标是(﹣1,d),
则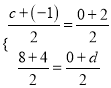 ,解得:
,解得: ![]() ,∴点F的坐标是(﹣1,12),点C的坐标是(3,0);
,∴点F的坐标是(﹣1,12),点C的坐标是(3,0);
综上,可得抛物线![]() 的对称轴上存在点F,使得以C、D、E、F为顶点的四边形为平行四边形,点F的坐标是(﹣1,4)、(﹣1,﹣4)或(﹣1,12).
的对称轴上存在点F,使得以C、D、E、F为顶点的四边形为平行四边形,点F的坐标是(﹣1,4)、(﹣1,﹣4)或(﹣1,12).
-
科目: 来源: 题型:
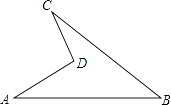
查看答案和解析>>【题目】如图是一块地,已知AD=4m,CD=3m,AB=13m,BC=12m,且CD⊥AD,求这块地的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校开展了“互助、平等、感恩、和谐、进取”主题班会活动,活动后,就活动的5个主题进行了抽样调查(每位同学只选最关注的一个),根据调查结果绘制了两幅不完整的统计图.根据图中提供的信息,解答下列问题:

(1)这次调查的学生共有多少名?
(2)请将条形统计图补充完整,并在扇形统计图中计算出“进取”所对应的圆心角的度数.
(3)如果要在这5个主题中任选两个进行调查,根据(2)中调查结果,用树状图或列表法,求恰好选到学生关注最多的两个主题的概率(将互助、平等、感恩、和谐、进取依次记为A、B、C、D、E).
-
科目: 来源: 题型:
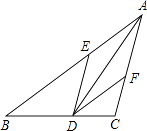
查看答案和解析>>【题目】如图,在△ABC中,AD是∠BAC的平分线,DE∥AC交AB于E,DF∥AB交AC于F,求证:四边形AEDF是菱形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】方程x(x﹣1)=0的解是( ).
A.x=1B.x=0C.x1=1,x2=0D.没有实数根
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的一元二次方程x2﹣mx﹣2m2=0.
(1)求证:不论m为何值,该方程总有两个实数根;
(2)若x=1是该方程的根,求代数式4m2+2m+5的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】宁都县某脐橙园2016年产量为1000吨,2018年产量为1440吨,求该脐橙园脐橙产量的年平均增长率,设该脐橙园脐橙产量的年平均增长量为x,则根据题意可列方程为_____.
相关试题

