【题目】如图,Rt△ABC中,AB=AC=8,BO=![]() AB,点M为BC边上一动点,将线段OM绕点O按逆时针方向旋转90°至ON,连接AN、CN,则△CAN周长的最小值为________.
AB,点M为BC边上一动点,将线段OM绕点O按逆时针方向旋转90°至ON,连接AN、CN,则△CAN周长的最小值为________.

参考答案:
【答案】8+4![]() .
.
【解析】
过点O作OB′⊥AB于点O,交BC于点B′,连接B′N并延长交AB于点E,易证△BOM≌△B′ON(SAS),∴点N始终在经过点B′且与BC垂直的射线上,因为△CAN周长=CA+AN+CN=8+ AN+CN,所以AN+CN值最小时,周长最小,属于最短路径问题,关键找点C关于B′E的对称点C′,连接A C′,与B′E的交点N′即为周长最小时的点N,此时AN+CN=AC′,求出AC′的值即可求出周长最小值.
解:过点O作OB′⊥AB于点O,交BC于点B′,连接B′N并延长交AB于点E,∵Rt△ABC中,AB=AC,
∴∠OBB′=45°=∠OB′B,OB =OB′
又∵∠BOB′=∠MON=90°
∴∠BOM=∠B′ON
∴△BOM≌△B′ON(SAS)
∴∠OBB′=45°=∠OB′N,即∠BB′N=90°,OB′= OB=2,BB′=2![]() ,
,
∴点N始终在经过点B′且与BC垂直的射线上,
易证△BB′E是等腰直角三角形,BE=4,即BE=AE,
∵△CAN周长=CA+AN+CN=8+ AN+CN
∴AN+CN值最小时,周长最小,属于最短路径问题,
∴找点C关于B′E的对称点C′,连接A C′,与B′E的交点N′即为周长最小时的点N,此时AN+CN=AC′,
等腰直角三角形△BB′E中, 由勾股定理得BB′=2![]() ,
,
等腰直角三角形△ABC中, BC=8![]() 由三线合一得:BD=DC=AD=
由三线合一得:BD=DC=AD=![]() BC=4
BC=4![]() ,
,
∴B′C=BC- BB′=8![]() -2
-2![]() =6
=6![]() ,由对称性得:B′C=B′C′=6
,由对称性得:B′C=B′C′=6![]() ,
,
∴C′D=12![]() -4
-4![]() =8
=8![]() ,
,
即:Rt△AC′D中,A C′=![]() =
=![]() =4
=4![]()
∴△CAN周长的最小值=8+ AN+CN=8+4.
-
科目: 来源: 题型:
查看答案和解析>>【题目】威丽商场销售A、B两种商品,售出1件A种商品和4件B种商品所得利润为600元;售出3件A种商品和5件B种商品所得利润为1100元.
(1)求每件A种商品和每件B种商品售出后所得利润分别为多少元?
(2)由于需求量大,A、B两种商品很快售完,威丽商场决定再一次购进A、B两种商品共34件,如果将这34件商品全部售完后所得利润不低于4000元,那么威丽商场至少需购进多少件A种商品?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
 中,
中, ,
, ,
, 为
为 边的中点,过点
边的中点,过点 作
作 交
交 的延长线于点
的延长线于点 ,
, 平分
平分 交
交 于点
于点 .
.
(1)求证:判断四边形
 的形状,并证明;
的形状,并证明;(2)若
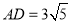 ,求
,求 及四边形
及四边形 的面积.
的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一段抛物线:y=﹣x(x﹣2)(0≤x≤2)记为C1,它与x轴交于两点O,A1;将C1绕A1旋转180°得到C2,交x轴于A2;将C2绕A2旋转180°得到C3,交x轴于A3;…如此进行下去,得到Cn,若点P(2017,m)在抛物线Cn上,则m为( )
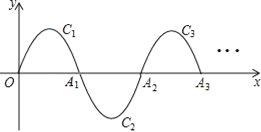
A. 1 B. ﹣1 C. 2 D. ﹣2
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,∠BAC=90°,AB=AC,D为△ABC外一点,且AD=AC,则∠BDC的度数为__________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在方格纸中,每个小正方形的边长为1,其中有两个格点A、B和直线l.
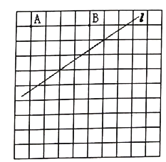
(1)在直线l上找一点M,使得MA=MB;
(2)找出点A关于直线l的对称点A1;
(3)P为直线l上一点,连接BP,AP,当△ABP周长最小时,画出点P的位置,并直接写出△ABP周长的最小值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了全面推进素质教育,增强学生体质,丰富校园文化生活,高新区某校将举行春季特色运动会,需购买A,B两种奖品.经市场调查,若购买A种奖品3件和B种奖品2件,共需60元;若购买A种奖品1件和B种奖品3件,共需55元.
(1)求A、B两种奖品的单价各是多少元;
(2)运动会组委会计划购买A、B两种奖品共100件,购买费用不超过1160元,且A种奖品的数量不大于B种奖品数量的3倍,运动会组委会共有几种购买方案?
(3)在第(2)问的条件下,设计出购买奖品总费用最少的方案,并求出最小总费用.
相关试题

