【题目】如图,在方格纸中,每个小正方形的边长为1,其中有两个格点A、B和直线l.
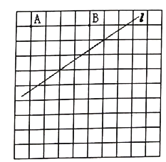
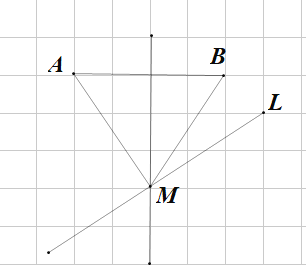
(1)在直线l上找一点M,使得MA=MB;
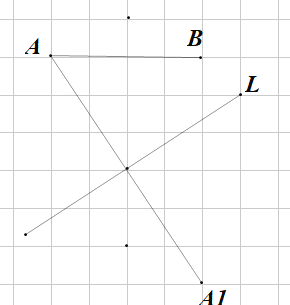
(2)找出点A关于直线l的对称点A1;
(3)P为直线l上一点,连接BP,AP,当△ABP周长最小时,画出点P的位置,并直接写出△ABP周长的最小值.
参考答案:
【答案】答案看详解.
【解析】
(1)连接AB,做AB的垂直平分线L1,L1与L相交于点M ,连接MA和MB,所以MA=MB.(2)过A点向L做垂线AO,并延长AO,使AO=A1O,即A1即为所求。(3)由(2)知A点关于L的对称点A1连接BA1与L相交于P, P点即为所求.
(1)
(2)
(3)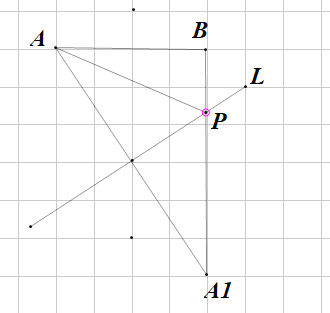
由图知:△ABP周长=AP+BP+AB=AB+BP+PA1=4+6=10,即△ABP周长的最小为10.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一段抛物线:y=﹣x(x﹣2)(0≤x≤2)记为C1,它与x轴交于两点O,A1;将C1绕A1旋转180°得到C2,交x轴于A2;将C2绕A2旋转180°得到C3,交x轴于A3;…如此进行下去,得到Cn,若点P(2017,m)在抛物线Cn上,则m为( )
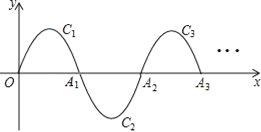
A. 1 B. ﹣1 C. 2 D. ﹣2
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,Rt△ABC中,AB=AC=8,BO=
 AB,点M为BC边上一动点,将线段OM绕点O按逆时针方向旋转90°至ON,连接AN、CN,则△CAN周长的最小值为________.
AB,点M为BC边上一动点,将线段OM绕点O按逆时针方向旋转90°至ON,连接AN、CN,则△CAN周长的最小值为________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,∠BAC=90°,AB=AC,D为△ABC外一点,且AD=AC,则∠BDC的度数为__________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了全面推进素质教育,增强学生体质,丰富校园文化生活,高新区某校将举行春季特色运动会,需购买A,B两种奖品.经市场调查,若购买A种奖品3件和B种奖品2件,共需60元;若购买A种奖品1件和B种奖品3件,共需55元.
(1)求A、B两种奖品的单价各是多少元;
(2)运动会组委会计划购买A、B两种奖品共100件,购买费用不超过1160元,且A种奖品的数量不大于B种奖品数量的3倍,运动会组委会共有几种购买方案?
(3)在第(2)问的条件下,设计出购买奖品总费用最少的方案,并求出最小总费用.
-
科目: 来源: 题型:
查看答案和解析>>【题目】解下列方程:(有指定方法必须用指定方法)
(1)
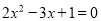 (配方法); (2)
(配方法); (2)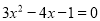 (公式法)
(公式法)(3)
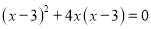 . (4)
. (4) .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知在△ABC中,AB=AC,BC=12厘米,点D为AB上一点且BD=8厘米,点P在线段BC上以2厘米/秒的速度由B点向C点运动,设运动时间为t,同时,点Q在线段CA上由C点向A点运动.

(1)用含t的式子表示PC的长为_______________;
(2)若点Q的运动速度与点p的运动速度相等,当t=2时,三角形BPD与三角形CQP是否全等,请说明理由;
(3)若点Q的运动速度与点P的运动速度不相等,请求出点Q的运动速度是多少时,能够使三角形BPD与三角形CQP全等?
相关试题

