【题目】已知:如图,∠B=90°AB∥DF,AB=3cm,BD=8cm,点C是线段BD上一动点,点E是直线DF上一动点,且始终保持AC⊥CE。
(1)试说明:∠ACB =∠CED
(2)当C为BD的中点时, ![]() ABC与
ABC与![]() EDC全等吗?若全等,请说明理由;若不全等,请改变BD的长(直接写出答案),使它们全等。
EDC全等吗?若全等,请说明理由;若不全等,请改变BD的长(直接写出答案),使它们全等。
(3)若AC=CE ,试求DE的长
(4)在线段BD的延长线上,是否存在点C,使得AC=CE,若存在,请求出DE的长及△AEC的面积;若不存在,请说明理由。



![]()
![]()
参考答案:
【答案】(1)见解析;(2)当C为BD中点时, ABC与 EDC不全等;(3)5cm;(4)见解析.
【解析】试题分析:(1)根据平行线的性质和三角形的内角和定理求出即可;
(2)根据全等三角形的判定定理进行判断,即可得出答案;
(3)根据全等得出对应边相等,即可得出答案;
(4)求出两三角形全等,得出对应边相等,再根据勾股定理和三角形面积公式求出即可.
试题解析:(1) ![]()
![]()
∵AC⊥CE,
![]()
![]()
![]()
(2)当C为BD的中点时,△ABC与△EDC不全等,当BD的长是6时,它们全等,
理由是:∵BD=6,C为BD中点,
∴BC=CD=3=AB,
在△ABC和△CDE中
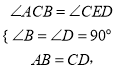
![]()
(3)∵在△ABC和△CDE中
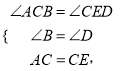
![]()
∴AB=CD=3cm,
∴DE=BC=8cm3cm=5cm;
(4)
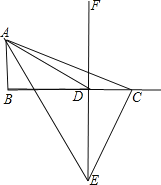
![]()
![]()
∵AC⊥CE,
![]()
![]()
∴∠ECD=∠BAC;
当CD=AB=3cm时,AC=CE,
∵在△ABC和△CDE中
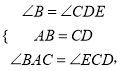
![]()
∴AC=CE,DE=BC=8cm,
∵AB=3cm,BC=BD+CD=8cm+3cm=11cm,
∴在![]() 中,由勾股定理得;
中,由勾股定理得; ![]()
![]()
∴△AEC的面积是![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】(本题7分)如图,点B、F、C、E在一条直线上,FB=CE,AC=DF,请从下列三个条件:①AB=DE;②∠A=∠D;③∠ACB=∠DFE中选择一个合适的条件,使AB∥ED成立,并给出证明.

(1)选择的条件是 (填序号)
(2)证明:
-
科目: 来源: 题型:
查看答案和解析>>【题目】两个大小不同的等腰直角三角板如图1所示放置,图2是由它抽象出的几何图形,B,C,E在同一条直线上,连结DC.

(1)请找出图2中的全等三角形,并给予证明(说明:结论中不得含有未标识的字母);
(2)指出线段DC和线段BE的关系,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线y=﹣
 ﹣x+4,
﹣x+4,(1)用配方法确定它的顶点坐标、对称轴;
(2)x取何值时,y随x增大而减小?
(3)x取何值时,抛物线在x轴上方?
-
科目: 来源: 题型:
查看答案和解析>>【题目】在一次函数y=kx+3中,y的值随着x值的增大而增大,请你写出符合条件的k的一个值: .
-
科目: 来源: 题型:
查看答案和解析>>【题目】解方程、计算
(1)
 (2)
(2)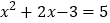 (限用配方法)
(限用配方法)(3) (x-2)
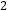 -5(x-2)-6=0 (4)计算、
-5(x-2)-6=0 (4)计算、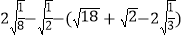
-
科目: 来源: 题型:
查看答案和解析>>【题目】设二次函数y1,y2的图象的顶点分别为(a,b)、(c,d),当a=﹣c,b=2d,且开口方向相同时,则称y1是y2的“反倍顶二次函数”.
(1)请写出二次函数y=x2+x+1的一个“反倍顶二次函数”;
(2)已知关于x的二次函数y1=x2+nx和二次函数y2=nx2+x,函数y1+y2恰是y1﹣y2的“反倍顶二次函数”,求n.
相关试题

