【题目】在平面直角坐标系中,一次函数y=ax+b(a≠0)的图象与反比例函数y= ![]() (k≠0)的图象交于第二、四象限内的A、B两点,与y轴交于C点,过点A作AH⊥y轴,垂足为H,OH=3,tan∠AOH=
(k≠0)的图象交于第二、四象限内的A、B两点,与y轴交于C点,过点A作AH⊥y轴,垂足为H,OH=3,tan∠AOH= ![]() ,点B的坐标为(m,﹣2).求:
,点B的坐标为(m,﹣2).求: 
(1)反比例函数和一次函数的解析式;
(2)写出当反比例函数的值大于一次函数的值时x的取值范围.
参考答案:
【答案】
(1)解:由OH=3,tan∠AOH= ![]() ,得AH=4.即A(﹣4,3),
,得AH=4.即A(﹣4,3),
将A点坐标代入y= ![]() (k≠0),得k=﹣4×3=﹣12.
(k≠0),得k=﹣4×3=﹣12.
反比例函数的解析式为y=﹣ ![]() .
.
将B点坐标代入y=﹣ ![]() 中,得﹣2=﹣
中,得﹣2=﹣ ![]() ,解得m=6.即B(6,﹣2),
,解得m=6.即B(6,﹣2),
将A、B两点坐标代入y=ax+b,得 ![]() ,解得
,解得  .
.
所以一次函数的解析式为y=﹣ ![]() x+1.
x+1.
(2)解:当反比例函数的值大于一次函数的值时,x的取值范围是﹣4<x<0或x>6.
【解析】(1)根据正切函数可得AH=4,根据反比例函数的特点k=xy为定值,列出方程,求出k的值,便可求出反比例函数的解析式;根据k的值求出B两点的坐标,用待定系数法便可求出一次函数的解析式.(2)根据函数图象可直接解答.
【考点精析】掌握解直角三角形是解答本题的根本,需要知道解直角三角形的依据:①边的关系a2+b2=c2;②角的关系:A+B=90°;③边角关系:三角函数的定义.(注意:尽量避免使用中间数据和除法).
-
科目: 来源: 题型:
查看答案和解析>>【题目】有一面积为5
 的等腰三角形,它的一个内角是30°,则以它的腰长为边的正方形的面积为 .
的等腰三角形,它的一个内角是30°,则以它的腰长为边的正方形的面积为 . -
科目: 来源: 题型:
查看答案和解析>>【题目】小彬和小明每天早晨坚持跑步,小彬每秒跑4米,小明每秒跑6米.
(1)如果他们站在百米跑道的两端同时相向起跑,那么几秒后两人相遇?
(2)如果小明站在百米跑道的起点处,小彬站在他前面10米处,两人同时同向起跑,几秒后小明能追上小彬?
(2)如果他们都站在四百米环形跑道的起点处,两人同时同向起跑,几分钟后他们再次相遇?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知有如下一组单项式:7x3z2,8x3y,
 x2yz,-3xy2z,9x4zy,zy2,-
x2yz,-3xy2z,9x4zy,zy2,- xyz,9y3z,xz2y,0,3z3.我们用下面的方法确定它们的先后次序:对任两个单项式,先看x的指数,规定x的指数高的单项式排在x的指数低的单项式前面;若x的指数相同,则再看y的指数,规定y的指数高的单项式排在y的指数低的单项式前面;若y的指数也相同,则再看z的指数,规定z的指数高的单项式排在z的指数低的单项式前面.将这组单项式按上述方法排序,那么,9y3z应排在第几位?
xyz,9y3z,xz2y,0,3z3.我们用下面的方法确定它们的先后次序:对任两个单项式,先看x的指数,规定x的指数高的单项式排在x的指数低的单项式前面;若x的指数相同,则再看y的指数,规定y的指数高的单项式排在y的指数低的单项式前面;若y的指数也相同,则再看z的指数,规定z的指数高的单项式排在z的指数低的单项式前面.将这组单项式按上述方法排序,那么,9y3z应排在第几位? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
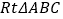 中,
中,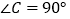 ,
,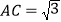 ,
,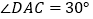 ,点D为BC边上一点,且BD=2AD,,求
,点D为BC边上一点,且BD=2AD,,求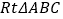 的周长(保留根号)。
的周长(保留根号)。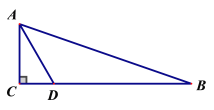
-
科目: 来源: 题型:
查看答案和解析>>【题目】“校园安全”受到全社会的广泛关注,某中学对部分学生就校园安全知识的了解程度,采用随机抽样调查的方式,并根据收集到的信息进行统计,绘制了两幅尚不完整的统计图,如图所示,请根据统计图中所提供的信息解答下列问题:
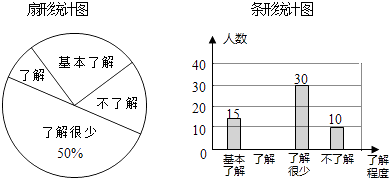
(1)接受问卷调查的学生共有人,扇形统计图中“基本了解”部分所对应扇形的圆心角为;
(2)请补全条形统计图;
(3)若从对校园安全知识达到了“了解”程度的3个女生和2个男生中随机抽取2人参加校园安全知识竞赛,请用树状图或列表法求出恰好抽到1个男生和1个女生的概率. -
科目: 来源: 题型:
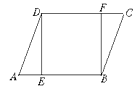
查看答案和解析>>【题目】如图,在平行四边ABCD中,E、F分别是AB、DC上的点,且AE=CF,
(1)求证:△ADE≌△CBF;
(2) 当∠DEB=90°时,试说明四边形DEBF为矩形.
相关试题

