【题目】小彬和小明每天早晨坚持跑步,小彬每秒跑4米,小明每秒跑6米.
(1)如果他们站在百米跑道的两端同时相向起跑,那么几秒后两人相遇?
(2)如果小明站在百米跑道的起点处,小彬站在他前面10米处,两人同时同向起跑,几秒后小明能追上小彬?
(2)如果他们都站在四百米环形跑道的起点处,两人同时同向起跑,几分钟后他们再次相遇?
参考答案:
【答案】(1)10秒后两人相遇;(2)5秒后小彬追上小明;(3)![]() 分钟后小彬追上小明.
分钟后小彬追上小明.
【解析】试题分析:(1)此问利用行程中的相遇问题解答,两人所行路程和等于总路程;
(2)(3)此问利用行程中的追及问题解答,两人所行路程差等于两人相距的路程.这两问利用最基本的数量关系:速度×时间=路程.
试题解析:解:(1)设x秒后两人相遇,根据题意得:6x+4x=100,
解得x=10;
答:10秒后两人相遇;
(2)解:设y秒后小彬追上小明,根据题意得:6y-4y=10,
解得y=5;
答:两人同时同向起跑,5秒后小彬追上小明.
(3)解:设a秒后小彬追上小明,根据题意得:6a-4a=400
解得a=200; 200秒=![]() 分钟
分钟
答:两人同时同向起跑, ![]() 分钟后小彬追上小明.
分钟后小彬追上小明.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠C=90°,以AC为一边向外作等边三角形ACD,点E为AB的中点,连结DE.
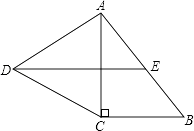
(1)证明DE∥CB;
(2)探索AC与AB满足怎样的数量关系时,四边形DCBE是平行四边形. -
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法正确的是( )
A.所有等边三角形都相似B.有一个角相等的两个等腰三角形相似
C.所有直角三角形都相似D.所有矩形都相似
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,点O是边AC上一个动点,过O作直线MN∥BC.设MN交∠ACB的平分线于点E,交∠ACB的外角平分线于点F.
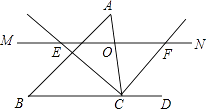
(1)求证:OE=OF;
(2)若CE=8,CF=6,求OC的长;
(3)当点O在边AC上运动到什么位置时,四边形AECF是矩形?并说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】满足下列条件的四边形不是正方形的是( )
A. 对角线相互垂直的矩形 B. 对角线相等的菱形
C. 对角线相互垂直且相等的四边形 D. 对角线垂直且相等的平行四边形
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,已知点A(1,2),B(2,1),C(﹣1,﹣3).D(﹣2,3),其中不可能与点E(1,3)在同一函数图象上的一个点是( )
A. 点A B. 点B C. 点C D. 点D
-
科目: 来源: 题型:
查看答案和解析>>【题目】按组成面的平和曲划分,与圆锥为同一类的几何体是( )
A.棱锥
B.棱柱
C.圆锥
D.长方体
相关试题

