【题目】如图,Rt△ABC中,AB⊥BC,AB=6,BC=4,P是△ABC内部的一个动点,且满足∠PAB=∠PBC,则线段CP长的最小值为 . 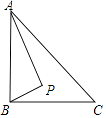
参考答案:
【答案】2
【解析】解:∵∠ABC=90°, ∴∠ABP+∠PBC=90°,
∵∠PAB=∠PBC
∴∠BAP+∠ABP=90°,
∴∠APB=90°,
∴点P在以AB为直径的⊙O上,连接OC交⊙O于点P,此时PC最小,
在RT△BCO中,∵∠OBC=90°,BC=4,OB=3,
∴OC= ![]() =5,
=5,
∴PC=OC=OP=5﹣3=2.
∴PC最小值为2.
故选B.
【考点精析】关于本题考查的相似三角形的判定与性质,需要了解相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方才能得出正确答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知点A(1,2)是反比例函数y=
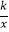 图象上的一点,连接AO并延长交双曲线的另一分支于点B,点P是x轴上一动点;若△PAB是等腰三角形,则点P的坐标是 .
图象上的一点,连接AO并延长交双曲线的另一分支于点B,点P是x轴上一动点;若△PAB是等腰三角形,则点P的坐标是 . 
-
科目: 来源: 题型:
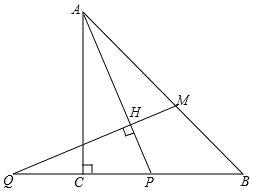
查看答案和解析>>【题目】如图,在等腰Rt△ABC中,角ACB=90°,P是线段BC上一动点(与点B,C不重合)连接AP,延长BC至点Q,使 CQ=CP,过点Q作QH⊥AP于点H,交AB于点M.
(1)∠APC=α,求∠AMQ的大小(用含α的式子表示);
(2)在(1)的条件下,过点M作ME⊥QB于点E,试证明 PC 与 ME 之间的数量关系,并证明.
-
科目: 来源: 题型:
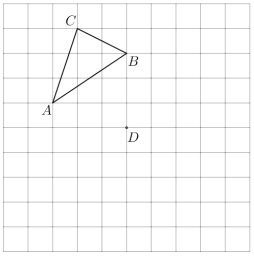
查看答案和解析>>【题目】在图中网格上按要求画出图形,并回答问题:
(1)如果将三角形
 平移,使得点
平移,使得点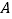 平移到图中点
平移到图中点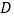 位置,点
位置,点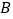 、点
、点 的对应点分别为点
的对应点分别为点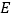 、点
、点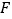 ,请画出三角形
,请画出三角形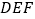 ;
;(2)画出三角形
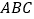 关于点
关于点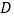 成中心对称的三角形
成中心对称的三角形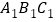 .
.(3)三角形
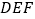 与三角形
与三角形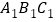 是否关于某个点成中心对称?如果是,请在图中画出这个对称中心,并记作点
是否关于某个点成中心对称?如果是,请在图中画出这个对称中心,并记作点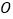 .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某市三景区是人们节假日游玩的热点景区,某学校对九(1)班学生“五一”小长假随父母到这三个景区游玩的计划做了全面调查,调查分四个类别,A:三个景区;B:游两个景区;C:游一个景区;D:不到这三个景区游玩,现根据调查结果绘制了不完全的条形统计图和扇形统计图如下:
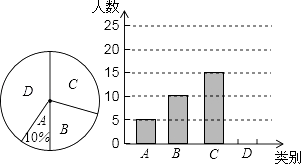
请结合图中信息解答下列问题:
(1)九(1)班现有学生人,在扇形统计图中表示“B类别”的扇形的圆心角的度数为;
(2)请将条形统计图补充完整;
(3)若该校九年级有1000名学生,求计划“五一”小长假随父母到这三个景区游玩的学生多少名? -
科目: 来源: 题型:
查看答案和解析>>【题目】学校准备购进一批节能灯,已知1只A型节能灯和3只B型节能灯共需26元;3只A型节能灯和2只B型节能灯共需29元.
(1)求一只A型节能灯和一只B型节能灯的售价各是多少元;
(2)学校准备购进这两种型号的节能灯共50只,并且A型节能灯的数量不多于B型节能灯数量的3倍,请设计出最省钱的购买方案,并说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AC为⊙O的直径,AB=BD,BD交AC于F,BE∥AD交AC的延长线于E点
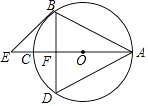
(1)求证:BE为⊙O的切线;
(2)若AF=4CF,求tan∠E.
相关试题

