【题目】如图,AC为⊙O的直径,AB=BD,BD交AC于F,BE∥AD交AC的延长线于E点 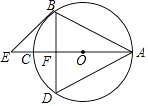
(1)求证:BE为⊙O的切线;
(2)若AF=4CF,求tan∠E.
参考答案:
【答案】
(1)解:如图,连接CD、OD、BO,延长BO交AD于点G,
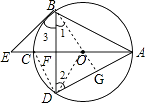
在△ABO和△DBO中,
∵ 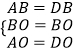 ,
,
∴△ABO≌△DBO(SSS),
∴∠1=∠ABO,
∴BG⊥AD,
∴∠1+∠2=90°,
∵BE∥AD,
∴∠2=∠3,
∴∠3+∠1=90°,即OB⊥BE,
∴BE为⊙O的切线
(2)解:设CF=x,则AF=4x,
∴AC=5x,OC=OB= ![]() AC=
AC= ![]() x,
x,
∴OF=OC﹣CF= ![]() x﹣x=
x﹣x= ![]() x,
x,
∵AC为⊙O的直径,
∴∠ADC=90°,
∴CD∥BG,
∴△CDF∽△OBF,
∴ ![]() =
= ![]() ,即
,即 ![]() =
= ![]() ,
,
则CD= ![]() x,
x,
∴AD= ![]() =
= ![]() =
= ![]() x,
x,
∵BE∥AD,
∴tanE=tan∠CAD= ![]() =
= ![]() =
= ![]()
【解析】(1)连接CD、OD、BO,延长BO交AD于点G,证△ABO≌△DBO得∠1=∠ABO,从而得BG⊥AD,即∠1+∠2=90°,根据∠2=∠3知∠3+∠1=90°,得证;(2)设CF=x,则AF=4x、OC=OB= ![]() AC=
AC= ![]() x、OF=OC﹣CF=
x、OF=OC﹣CF= ![]() x,证△CDF∽△OBF得
x,证△CDF∽△OBF得 ![]() =
= ![]() ,从而求得CD=
,从而求得CD= ![]() x、AD=
x、AD= ![]() =
= ![]() x,由tanE=tan∠CAD=
x,由tanE=tan∠CAD= ![]() 可得答案.
可得答案.
【考点精析】关于本题考查的切线的判定定理和解直角三角形,需要了解切线的判定方法:经过半径外端并且垂直于这条半径的直线是圆的切线;解直角三角形的依据:①边的关系a2+b2=c2;②角的关系:A+B=90°;③边角关系:三角函数的定义.(注意:尽量避免使用中间数据和除法)才能得出正确答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,Rt△ABC中,AB⊥BC,AB=6,BC=4,P是△ABC内部的一个动点,且满足∠PAB=∠PBC,则线段CP长的最小值为 .
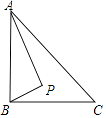
-
科目: 来源: 题型:
查看答案和解析>>【题目】某市三景区是人们节假日游玩的热点景区,某学校对九(1)班学生“五一”小长假随父母到这三个景区游玩的计划做了全面调查,调查分四个类别,A:三个景区;B:游两个景区;C:游一个景区;D:不到这三个景区游玩,现根据调查结果绘制了不完全的条形统计图和扇形统计图如下:
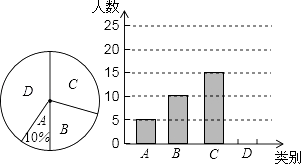
请结合图中信息解答下列问题:
(1)九(1)班现有学生人,在扇形统计图中表示“B类别”的扇形的圆心角的度数为;
(2)请将条形统计图补充完整;
(3)若该校九年级有1000名学生,求计划“五一”小长假随父母到这三个景区游玩的学生多少名? -
科目: 来源: 题型:
查看答案和解析>>【题目】学校准备购进一批节能灯,已知1只A型节能灯和3只B型节能灯共需26元;3只A型节能灯和2只B型节能灯共需29元.
(1)求一只A型节能灯和一只B型节能灯的售价各是多少元;
(2)学校准备购进这两种型号的节能灯共50只,并且A型节能灯的数量不多于B型节能灯数量的3倍,请设计出最省钱的购买方案,并说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】依法纳税是每个公民应尽的义务.新税法规定:居民个人的综合所得,以每一纳税月收入减去费用5000元以及专项扣除、专项附加扣除和依法确定的其它扣除后的余额,为个人应纳税所得额.已知李先生某月的个人应纳税所得额比张先生的多1500元,个人所得税税率相同情况下,李先生的个人所得税税额为76.5元,而张先生的个人所得税税额为31.5元.求李先生和张先生应纳税所得额分别为多少元?
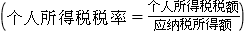
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知一张长方形纸片,
 ,
, (
( ).将这张纸片沿着过点
).将这张纸片沿着过点 的折痕翻折,使点
的折痕翻折,使点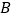 落在
落在 边上的点
边上的点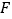 ,折痕交
,折痕交 于点
于点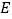 ,将折叠后的纸片再次沿着另一条过点
,将折叠后的纸片再次沿着另一条过点 的折痕翻折,点
的折痕翻折,点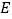 恰好与点
恰好与点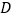 重合,此时折痕交
重合,此时折痕交 于点
于点 .
.(1)在图中确定点
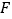 、点
、点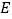 和点
和点 的位置;
的位置;(2)联结
 , 则
, 则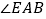 等于多少°;
等于多少°;(3)用含有
 、
、 的代数式表示线段
的代数式表示线段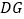 的长.
的长.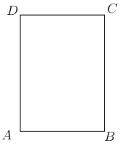
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算下列各题
(1)3b﹣2a2﹣(﹣4a+a2+3b)+a2;
(2)﹣13﹣(1﹣
 )×
)× ×[2﹣(﹣3)2];
×[2﹣(﹣3)2];(3)﹣|﹣23|+15﹣|4.5﹣(﹣2.5)|;
(4)89′25″﹣48′58″;
(5)化简求值:5(3a2b﹣ab2)﹣(ab2+3a2b),其中a=
 ,b=
,b= .
.
相关试题

