【题目】如图，在平面直角坐标系中，已知点A（-5,0），B（5,0），

（1）写出C点的坐标；

（2）动点P从B点出发以每秒1个单位的速度沿BA方向运动，同时动点Q从C点出发也以每秒1个单位的速度沿y轴正半轴方向运动（当P点运动到A点时，两点都停止运动）.设从出发起运动了x秒.

①请用含x的代数式分别表示P,Q两点的坐标；

②当x=2时，y轴上是否存在一点E，使得△AQE的面积与△APQ的面积相等？若存在，求E的坐标，若不存在，说明理由？

（3）在点P、Q运动过程中，过点Q作x轴的平行线DE，∠DQP与∠APQ的角平分线交于点M，则∠PMQ的大小会随点P、Q的运动而变化吗？如果不变化，请求出∠PMQ的度数；若发生变化，请说明理由。

参考答案：

【答案】（1）C(0，5)；（2）①P(5-x,0) Q(0,5+x)；②Q(0，18.2)或（0，-4.2）；（3）不变，理由见解析.

【解析】试题分析：（1）根据y轴上点的坐标特征写出即可；

（2）①点P沿x轴向左运动，用起始位置的横坐标5减去运动的长度x，纵坐标不变；点Q沿y轴向上运动，用起始位置的纵坐标5加上运动的长度x，横坐标不变；②先求出P、Q的坐标和△APQ的面积，分E在y轴的正半轴和E在y轴的负半轴两种情况,根据三角形的面积公式计算即可；

（3）由DE∥AB得 ∠DQP+∠APQ=180，由QM、PM分别是∠DQP与∠APQ的角平分线得 ∠MQP+∠MPQ=90，根据三角形内角和可知 ∠PMQ=90.

解：（1）由图得，C(0，5)

（2）①由题意得，P(5-x,0) Q(0,5+x)

②当x=2时，P(3,0) Q(0,7)

△APQ的面积=28

因为△AQE的高为：5，所以底边 QE=11.2

所以：Q(0，18.2)或（0，-4.2）

（3）不变。 如图，

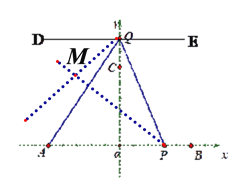
∵DE∥AB，

∴ ∠DQP+∠APQ=180，

∵QM、PM分别是∠DQP与∠APQ的角平分线，

∴ ∠MQP+∠MPQ=90 ，

∴ ∠PMQ=90.

关闭