【题目】如图,△ABC中,AB=AC,∠A=36°,DE垂直平分AB交AC于D,交AB于E,下列论述错误的是( )

A. BD平分∠ABC B. D是AC的中点
C. AD=BD=BC D. △BDC的周长等于AB+BC
参考答案:
【答案】B
【解析】试题解析:A、∵△ABC中,AB=AC,∠A=36°,AB的中垂线DE交AC与D,交AB于E,
∴∠ABC=∠ACB=![]() (180°-∠A)=
(180°-∠A)=![]() (180°-36°)=72°
(180°-36°)=72°
AD=BD,即∠A=∠ABD=36°
∴∠DBC=∠ABC-∠ABD=72°-36°=36°,故A正确;
B、条件不足,不能证明,故不对;
C、∵∠DBC=36°,∠C=72°
∴∠BDC=180°-72°-36°=72°,∠C=∠BDC
∵AD=BD
∴AD=BD=BC故C正确;
D、∵AD=BD
∴△BDC的周长等于AB+BC
故D正确;
故选B.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,Rt△ABC和Rt△DBE中,∠ABC=∠EBD=90°,AB=BC,DB=EB.显然可得结论AD=EC,AD⊥EC.
(1)阅读:当Rt△DBE绕点B逆时针旋转到图2的位置时,连接AD,CE.求证:AD=EC,AD⊥EC.
下面给出了小亮的证明过程,请你把小亮的证明过程填写完整:
∵∠ABC=∠EBD,∴∠ABC-∠ABE=∠EBD-∠ABE,即∠EBC=∠DBA.在△EBC和△DBA中,
BC=BA,∠______=∠______,BE=BD,
∴△EBC≌△DBA,∴CE=AD,∠ECB=∠______.
∵∠ECB+∠ACE+∠CAB=90°,∴∠DAB+∠ACE+∠CAB=90°,∴∠______=90°,∴AD⊥EC.
(2)类比:当Rt△DBE绕点B逆时针旋转90°得到图3时,连接AD,CE.问(1)中线段AD,EC间的数量关系和位置关系还成立吗?若成立,请给出证明;若不成立,请说明理由;
(3)拓展:当Rt△DBE绕点B逆时针旋转到图4时,连接AD,CE.请说明AD,EC间的数量关系和位置关系.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC中,AB=AC,点D在底边BC上,添加下列条件后,仍无法判定△ABD≌△ACD的是( )

A. BD=CD B. ∠BAD=∠CAD C. ∠B=∠C D. ∠ADB=∠ADC
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,若每个小正方形的边长均为1,试解决以下问题:

(1)图中阴影部分的面积是多少?
(2)阴影部分正方形的边长是多少?
(3)估计边长的值在哪两个整数之间?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某市居民生活用水的费用由“城市供水费” 和“污水处理费” 两部分组成.为了鼓励市民节约用水,其中城市供水费按阶梯式计费:一个月用水10吨以内(包括10吨)的用户,每吨收1.5元;一个月用水超过10吨的用户,10吨水仍按每吨1.5元收费,超过10吨的部分,按每吨2元收费.另外污水处理费按每吨0.65元收取.
(1)某居民5月份用水8吨,应交水费多少元? 6月份用水12吨,应交水费多少元?
(2)若某户某月用水x吨,请你用含有x的代数式表示该月应交的水费.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形ABCD中,AB=8,BC=6,点E在边AB上,点F在边CD上,点G、H在对角线AC上,若四边形EGFH是菱形,则AE的长是( )

A.6
B.6.25
C.6.5
D.7 -
科目: 来源: 题型:
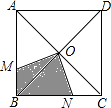
查看答案和解析>>【题目】如图,一只蚂蚁在正方形ABCD区域内爬行,点O是对角线的交点,∠MON=90°,OM,ON分别交线段AB,BC于M,N两点,则蚂蚁停留在阴影区域的概率为 .
相关试题

