【题目】如图,若每个小正方形的边长均为1,试解决以下问题:

(1)图中阴影部分的面积是多少?
(2)阴影部分正方形的边长是多少?
(3)估计边长的值在哪两个整数之间?
参考答案:
【答案】(1)10(2)![]() (3)
(3)![]()
【解析】
(1)将阴影部分的面积分割为一个小正方形和四个小直角三角形来求;
(2)在直角三角形中,利用勾股定理来计算斜边的长即可;
(3)利用“夹逼法”来估算无理数的大小.
如图所示:
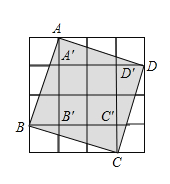
(1)S阴影=S正方形A′B′C′D′+S△BCC′+S△ABB′+S△ADA′+S△DCD′,
=2×2+![]() ×4×(1×3),
×4×(1×3),
=4+6,
=10;
(2)在直角三角形AA′D中,
AA′=1,A′D=3,
∴AD=![]() =
=![]() ,
,
即阴影部分的边长为![]() ;
;
(3)∵9<10<16,
∴3<![]() <4,即边长的值在3与4之间.
<4,即边长的值在3与4之间.
-
科目: 来源: 题型:
查看答案和解析>>【题目】五边形的顶点依次编号为1,2,3,4,5.若从某一顶点开始,沿正五边形的边顺时针方向行走,顶点编号的数字是几,就走几个边长,则称这种走法为一次“移位”.如:小宇在编号为3的顶点上时,那么他应走3个边长,即从3→4→5→1为第一次“移位”,这时他到达编号为1的顶点;然后从1→2为第二次“移位”.若小宇从编号为4的顶点开始,第2018次“移位”后,那么他所处的顶点的编号是( )

A. 1 B. 2 C. 3 D. 4
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,Rt△ABC和Rt△DBE中,∠ABC=∠EBD=90°,AB=BC,DB=EB.显然可得结论AD=EC,AD⊥EC.
(1)阅读:当Rt△DBE绕点B逆时针旋转到图2的位置时,连接AD,CE.求证:AD=EC,AD⊥EC.
下面给出了小亮的证明过程,请你把小亮的证明过程填写完整:
∵∠ABC=∠EBD,∴∠ABC-∠ABE=∠EBD-∠ABE,即∠EBC=∠DBA.在△EBC和△DBA中,
BC=BA,∠______=∠______,BE=BD,
∴△EBC≌△DBA,∴CE=AD,∠ECB=∠______.
∵∠ECB+∠ACE+∠CAB=90°,∴∠DAB+∠ACE+∠CAB=90°,∴∠______=90°,∴AD⊥EC.
(2)类比:当Rt△DBE绕点B逆时针旋转90°得到图3时,连接AD,CE.问(1)中线段AD,EC间的数量关系和位置关系还成立吗?若成立,请给出证明;若不成立,请说明理由;
(3)拓展:当Rt△DBE绕点B逆时针旋转到图4时,连接AD,CE.请说明AD,EC间的数量关系和位置关系.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC中,AB=AC,点D在底边BC上,添加下列条件后,仍无法判定△ABD≌△ACD的是( )

A. BD=CD B. ∠BAD=∠CAD C. ∠B=∠C D. ∠ADB=∠ADC
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,AB=AC,∠A=36°,DE垂直平分AB交AC于D,交AB于E,下列论述错误的是( )

A. BD平分∠ABC B. D是AC的中点
C. AD=BD=BC D. △BDC的周长等于AB+BC
-
科目: 来源: 题型:
查看答案和解析>>【题目】某市居民生活用水的费用由“城市供水费” 和“污水处理费” 两部分组成.为了鼓励市民节约用水,其中城市供水费按阶梯式计费:一个月用水10吨以内(包括10吨)的用户,每吨收1.5元;一个月用水超过10吨的用户,10吨水仍按每吨1.5元收费,超过10吨的部分,按每吨2元收费.另外污水处理费按每吨0.65元收取.
(1)某居民5月份用水8吨,应交水费多少元? 6月份用水12吨,应交水费多少元?
(2)若某户某月用水x吨,请你用含有x的代数式表示该月应交的水费.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形ABCD中,AB=8,BC=6,点E在边AB上,点F在边CD上,点G、H在对角线AC上,若四边形EGFH是菱形,则AE的长是( )

A.6
B.6.25
C.6.5
D.7
相关试题

