【题目】如图,矩形ABCD中,AB=8,BC=6,点E在边AB上,点F在边CD上,点G、H在对角线AC上,若四边形EGFH是菱形,则AE的长是( ) 
A.6
B.6.25
C.6.5
D.7
参考答案:
【答案】B
【解析】解:连接EF交AC于O, ∵四边形EGFH是菱形,
∴EF⊥AC,OE=OF,
∵四边形ABCD是矩形,
∴∠B=∠D=90°,AB∥CD,
∴∠ACD=∠CAB,
在△CFO与△AOE中, ,
,
∴△CFO≌△AOE(AAS),
∴AO=CO,
∵AC= ![]() =10,
=10,
∴AO= ![]() AC=5,
AC=5,
∵∠CAB=∠CAB,∠AOE=∠B=90°,
∴△AOE∽△ABC,
∴ ![]() ,
,
∴ ![]() =
= ![]() ,
,
∴AE= ![]() =6.25.
=6.25.
故选:B.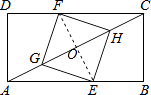
【考点精析】根据题目的已知条件,利用菱形的性质和矩形的性质的相关知识可以得到问题的答案,需要掌握菱形的四条边都相等;菱形的对角线互相垂直,并且每一条对角线平分一组对角;菱形被两条对角线分成四个全等的直角三角形;菱形的面积等于两条对角线长的积的一半;矩形的四个角都是直角,矩形的对角线相等.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,若每个小正方形的边长均为1,试解决以下问题:

(1)图中阴影部分的面积是多少?
(2)阴影部分正方形的边长是多少?
(3)估计边长的值在哪两个整数之间?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,AB=AC,∠A=36°,DE垂直平分AB交AC于D,交AB于E,下列论述错误的是( )

A. BD平分∠ABC B. D是AC的中点
C. AD=BD=BC D. △BDC的周长等于AB+BC
-
科目: 来源: 题型:
查看答案和解析>>【题目】某市居民生活用水的费用由“城市供水费” 和“污水处理费” 两部分组成.为了鼓励市民节约用水,其中城市供水费按阶梯式计费:一个月用水10吨以内(包括10吨)的用户,每吨收1.5元;一个月用水超过10吨的用户,10吨水仍按每吨1.5元收费,超过10吨的部分,按每吨2元收费.另外污水处理费按每吨0.65元收取.
(1)某居民5月份用水8吨,应交水费多少元? 6月份用水12吨,应交水费多少元?
(2)若某户某月用水x吨,请你用含有x的代数式表示该月应交的水费.
-
科目: 来源: 题型:
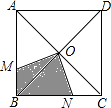
查看答案和解析>>【题目】如图,一只蚂蚁在正方形ABCD区域内爬行,点O是对角线的交点,∠MON=90°,OM,ON分别交线段AB,BC于M,N两点,则蚂蚁停留在阴影区域的概率为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)23﹣6×(﹣3)+2×(﹣4) ; (2)﹣16﹣(﹣5)+23﹣|﹣
 |
|(3)﹣(1﹣0.5)÷
 ×[2+(﹣4)2].
×[2+(﹣4)2].(4)(4)﹣22﹣(﹣
 )2×
)2× +6÷|
+6÷| ﹣2|+(﹣1)5×(﹣
﹣2|+(﹣1)5×(﹣ )2.
)2. -
科目: 来源: 题型:
查看答案和解析>>【题目】我们知道,
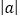 可以理解为
可以理解为 ,它表示:数轴上表示数a的点到原点的距离,这是绝对值的几何意义。进一步地,数轴上的两个点A,B分别用数
,它表示:数轴上表示数a的点到原点的距离,这是绝对值的几何意义。进一步地,数轴上的两个点A,B分别用数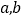 表示,那么A,B两点之间的距离为
表示,那么A,B两点之间的距离为 ,反过来,式子
,反过来,式子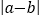 的几何意义是:数轴上表示数
的几何意义是:数轴上表示数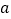 的点和表示数
的点和表示数 的点之间的距离。利用此结论,
的点之间的距离。利用此结论,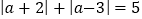 的意义就是数轴上表示数
的意义就是数轴上表示数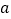 的点到表示-2和表示3的点的距离之和是5,若
的点到表示-2和表示3的点的距离之和是5,若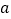 是整数,则符合
是整数,则符合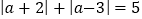 的
的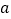 的个数是( )
的个数是( )A. 6 B. 5 C. 4 D. 3
相关试题

