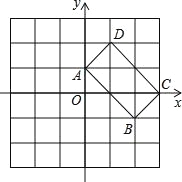
[题目]如图.在 6×6 的网格中.四边形 ABCD 的顶点都在格点上.每个格子都是边长为 1 的正方形.建立如图所示的平面直角坐标系．(1)画出四边形 ABCD 关于 y 轴对称和四边形 A′B′C′D′(点 A.B.C.D的对称点分别是点 A′B′C′D′．(2)求 A.B′.B.C 四点组成和四边形的面积．题目和参考答案 ——青夏教育精英家教网—

【题目】如图，在 6×6 的网格中，四边形 ABCD 的顶点都在格点上，每个格子都是边长为 1 的正方形，建立如图所示的平面直角坐标系．

（1）画出四边形 ABCD 关于 y 轴对称和四边形 A′B′C′D′（点 A、B、C、D的对称点分别是点 A′B′C′D′．

（2）求 A、B′、B、C 四点组成和四边形的面积．

参考答案：

【答案】（1）四边形 A′B′C′D′如图所示见解析；（2）6.

【解析】

（1）根据网格结构找出B、C、D关于y轴的对称点,依次连接对称点即可解题,

（2）利用四边形所在矩形面积减去四周三个小直角三角形面积,列式计算即可.

（1）四边形 A′B′C′D′如图所示；

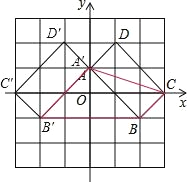
（2）四边形 AB′BC 的面积＝5×2﹣×2×2﹣×1×1﹣×1×3，

＝10﹣2﹣﹣，

＝10﹣4，

＝6．

相关试题

科目： 来源： 题型：

【题目】小伟和小欣玩一种抽卡片游戏：将背面完全相同、正面分别写有1，2，3，4的四张卡片背面向上洗匀后，小伟和小欣各自随机抽取一张（不放回）．将小伟的数字作为十位数字，小欣的数字作为个位数字，组成一个两位数．如果所组成的两位数为偶数，则小伟胜；否则小欣胜．
（1）当小伟抽取的卡片数字为2时，问两人谁获胜的可能性大？
（2）通过计算判断这个游戏对小伟和小欣是否公平．
查看答案和解析>>
科目： 来源： 题型：

【题目】按要求画图，并回答问题：
如图，在同一平面内有三点A，B，C．
(1)画直线AC；
(2)画射线CB；
(3)过点B作直线AC的垂线BD，垂足为D；
(4)画线段AB及线段AB的中点E，连接DE；
(5)通过画图和测量，与线段DE长度相等的线段有__________．
查看答案和解析>>
科目： 来源： 题型：

【题目】如图1，矩形铁片ABCD的长为2a，宽为a；为了要让铁片能穿过直径为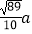的圆孔，需对铁片进行处理（规定铁片与圆孔有接触时铁片不能穿过圆孔）；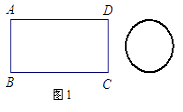
（1）如图2，M、N、P、Q分别是AD、AB、BC、CD的中点，若将矩形铁片的四个角去掉，只余下四边形MNPQ， ①则此时铁片是什么形状；
②给出证明，并通过计算说明此时铁片都能穿过圆孔；

（2）如图3，过矩形铁片ABCD的中心作一条直线分别交边BC、AD于点E、F（不与端点重合），沿着这条直线将矩形铁片切割成两个全等的直角梯形铁片；
①当BE=DF=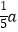 时，判断直角梯形铁片EBAF能否穿过圆孔，并说明理由；
②为了能使直角梯形铁片EBAF顺利穿过圆孔，请直接写出线段BE的长度的取值范围．
查看答案和解析>>
科目： 来源： 题型：

【题目】对于数轴上的点P，Q，给出如下定义：若点P到点Q的距离为d(d≥0)，则称d为点P到点Q的d追随值，记作d[PQ]．例如，在数轴上点P表示的数是2，点Q表示的数是5，则点P到点Q的d追随值为d[PQ]=3．
问题解决：
(1)点M，N都在数轴上，点M表示的数是1，且点N到点M的d追随值d[MN]=a(a≥0)，则点N表示的数是_____(用含a的代数式表示)；
(2)如图，点C表示的数是1，在数轴上有两个动点A，B都沿着正方向同时移动，其中A点的速度为每秒3个单位，B点的速度为每秒1个单位，点A从点C出发，点B表示的数是b，设运动时间为t(t>0)．
①当b=4时，问t为何值时，点A到点B的d追随值d[AB]=2；
②若0<t≤3时，点A到点B的d追随值d[AB]≤6，求b的取值范围．
查看答案和解析>>
科目： 来源： 题型：

【题目】如图，在△ABC 中，AB＝AC，∠BAC＝120°，D 为 BC 的中点，DE⊥AC 于点 E，AE＝8，求 CE 的长．
查看答案和解析>>
科目： 来源： 题型：

【题目】如图，已知抛物线y=x2+bx+c与x轴交于A、B两点（A点在B点左侧），与y轴交于点C（0，﹣3），对称轴是直线x=1，直线BC与抛物线的对称轴交于点D．

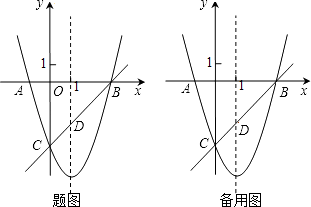
（1）求抛物线的函数表达式；
（2）求直线BC的函数表达式；
（3）点E为y轴上一动点，CE的垂直平分线交CE于点F，交抛物线于P、Q两点，且点P在第三象限．
①当线段PQ= AB时，求tan∠CED的值；
②当以点C、D、E为顶点的三角形是直角三角形时，请直接写出点P的坐标．
温馨提示：考生可以根据第（3）问的题意，在图中补出图形，以便作答．
查看答案和解析>>