【题目】小伟和小欣玩一种抽卡片游戏:将背面完全相同、正面分别写有1,2,3,4的四张卡片背面向上洗匀后,小伟和小欣各自随机抽取一张(不放回).将小伟的数字作为十位数字,小欣的数字作为个位数字,组成一个两位数.如果所组成的两位数为偶数,则小伟胜;否则小欣胜.
(1)当小伟抽取的卡片数字为2时,问两人谁获胜的可能性大?
(2)通过计算判断这个游戏对小伟和小欣是否公平.
参考答案:
【答案】
(1)解:列表得:
数字 | 1 | 2 | 3 | 4 |
1 | ﹣﹣﹣ | 12 | 13 | 14 |
2 | 21 | ﹣﹣﹣ | 23 | 24 |
3 | 31 | 32 | ﹣﹣﹣ | 34 |
4 | 41 | 42 | 43 | ﹣﹣﹣ |
共有3种等可能的情况数,其中P(小伟胜)= ![]() ,P(小欣胜)=
,P(小欣胜)= ![]() ,
,
∴小欣获胜的可能性大.
(2)解:这个游戏对小伟和小欣是公平的.理由如下:
由(1)可知共有12种等可能结果,其中偶数占6个,奇数占6个,
∴P(小伟胜)= ![]() ,P(小欣胜)=
,P(小欣胜)= ![]() ,
,
∴这个游戏对小伟和小欣是公平的.
【解析】(1)找出十位数字为2的所有等可能的情况数,进而求出两人获胜的概率,比较即可得到结果;(2)这个游戏对小伟和小欣是公平的.根据题意,由(1)的图表,分别计算两人谁获胜的可能性,比较可得答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】嫦娥四号探测器于2019年1月3日,成功着陆在月球背面,通过“鹊桥”中继星传回了世界第一张近距离拍摄的月背影像图,开启了人类月球探测新篇章.当中继星成功运行于地月拉格朗日L2点时,它距离地球约1500000km.用科学记数法表示数1500000为( )

A. 15×105 B. 1.5×106 C. 0.15×107 D. 1.5×105
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,Rt△ABC中,直角边AC=7cm,BC=3cm,CD为斜边AB上的高,点E从点B出发沿直线BC以2cm/s的速度移动,过点E作BC的垂线交直线CD于点F.
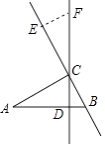
(1)求证:∠A=∠BCD;
(2)点E运动多长时间,CF=AB?并说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点O是直线AB上一点,∠BOC=120°,OD平分∠AOC.
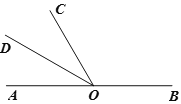
(1)求∠COD的度数.
请你补全下列解题过程.
∵点O为直线AB上一点,
∴∠AOB=_____.
∵∠BOC =120°,
∴∠AOC=______.
∵OD 平分∠AOC,
∴∠COD=
 ∠AOC.( )
∠AOC.( )∴∠COD=________.
(2)若E是直线AB外一点,满足∠COE:∠BOE=4:1直接写出∠BOE的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】按要求画图,并回答问题:
如图,在同一平面内有三点A,B,C.

(1)画直线AC;
(2)画射线CB;
(3)过点B作直线AC的垂线BD,垂足为D;
(4)画线段AB及线段AB的中点E,连接DE;
(5)通过画图和测量,与线段DE长度相等的线段有__________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,矩形铁片ABCD的长为2a,宽为a; 为了要让铁片能穿过直径为
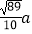 的圆孔,需对铁片进行处理(规定铁片与圆孔有接触时铁片不能穿过圆孔);
的圆孔,需对铁片进行处理(规定铁片与圆孔有接触时铁片不能穿过圆孔); 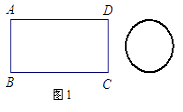
(1)如图2,M、N、P、Q分别是AD、AB、BC、CD的中点,若将矩形铁片的四个角去掉,只余下四边形MNPQ, ①则此时铁片是什么形状;
②给出证明,并通过计算说明此时铁片都能穿过圆孔;
(2)如图3,过矩形铁片ABCD的中心作一条直线分别交边BC、AD于点E、F(不与端点重合),沿着这条直线将矩形铁片切割成两个全等的直角梯形铁片;
①当BE=DF=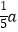 时,判断直角梯形铁片EBAF能否穿过圆孔,并说明理由;
时,判断直角梯形铁片EBAF能否穿过圆孔,并说明理由;
②为了能使直角梯形铁片EBAF顺利穿过圆孔,请直接写出线段BE的长度的取值范围. -
科目: 来源: 题型:
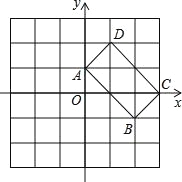
查看答案和解析>>【题目】如图,在 6×6 的网格中,四边形 ABCD 的顶点都在格点上,每个格子都是边长为 1 的正方形,建立如图所示的平面直角坐标系.
(1)画出四边形 ABCD 关于 y 轴对称和四边形 A′B′C′D′(点 A、B、C、D的对称点分别是点 A′B′C′D′.
(2)求 A、B′、B、C 四点组成和四边形的面积.
相关试题

