【题目】如图,已知关于x的一元二次方程x2+2x+![]() =0有两个不相等的实数根,k为正整数.
=0有两个不相等的实数根,k为正整数.
(1)求k的值;
(2)当此方程有一根为零时,直线y=x+2与关于x的二次函数y=x2+2x+![]() 的图象交于A、B两点,若M是线段AB上的一个动点,过点M作MN⊥x轴,交二次函数的图象于点N,求线段MN的最大值.
的图象交于A、B两点,若M是线段AB上的一个动点,过点M作MN⊥x轴,交二次函数的图象于点N,求线段MN的最大值.

参考答案:
【答案】(1)k=1或2;(2)当t=﹣![]() 时,MN有最大值,最大值为
时,MN有最大值,最大值为![]() .
.
【解析】
(1)、根据方程有两个不相等的实数根得出△>0,从而得出k的取值范围,然后根据k为正整数,从而得出k的值;(2)、将x=0代入方程求出k的值,从而得出函数解析式,解出函数的交点坐标,设M(t,t+2)(﹣2<t<1),则N(t,t2+2t),然后根据长度的计算法则得出函数解析式,从而得出最大值.
(1)根据题意得△=22﹣4×![]() >0,解得k<3,而k为正整数, 所以k=1或2;
>0,解得k<3,而k为正整数, 所以k=1或2;
(2)当x=0代入x2+2x+![]() =0得k=1,则方程为x2+2x=0, 二次函数为y=x2+2x,
=0得k=1,则方程为x2+2x=0, 二次函数为y=x2+2x,
解方程组![]() 得
得![]() 或
或![]() ,则A(﹣2,0),B(1,3),
,则A(﹣2,0),B(1,3),
设M(t,t+2)(﹣2<t<1),则N(t,t2+2t),
所以MN=t+2﹣(t2+2t)=﹣t2﹣t+2=﹣(t+![]() )2+
)2+![]() ,
,
当t=﹣![]() 时,MN有最大值,最大值为
时,MN有最大值,最大值为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在直角坐标平面内,已点A(3,0)、B(-5,3),将点A向左平移6个单位到达C点,将点B向下平移6个单位到达D点.
(1)写出C点、D点的坐标:C __________,D ____________ ;
(2)把这些点按A-B-C-D-A顺次连接起来,这个图形的面积是__________.

-
科目: 来源: 题型:
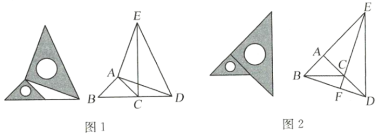
查看答案和解析>>【题目】把两个大小不同的等腰直角三角板按照一定的规则放置:“在同一平面内将直角顶点叠合”.
(1)图1是一种放置位置及由它抽象出的几何图形,
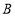 、
、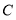 、
、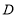 在同一条直线上,联结
在同一条直线上,联结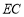 . 请找出图中的全等三角形(结论中不含未标识的字母),并说明理由;
. 请找出图中的全等三角形(结论中不含未标识的字母),并说明理由;(2)图2也是一种放置位置及由它抽象出的几何图形,
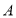 、
、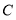 、
、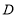 在同一条直线上,联结
在同一条直线上,联结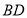 、
、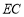 ,并延长
,并延长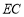 与
与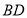 交于点
交于点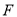 .请找出线段
.请找出线段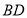 和
和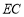 的位置关系,并说明理由;
的位置关系,并说明理由;(3)请你:
①画出一个符合放置规则且不同于图1和图2所放位置的几何图形;
②写出你所画几何图形中线段
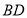 和
和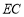 的位置和数量关系;
的位置和数量关系;③上面第②题中的结论在按照规则放置所抽象出的几何图形中都存在吗?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平行四边形
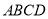 中,∠D=100°,∠DAB的平分线AE交DC于点E,连接BE,若AE=AB,则∠EBC的度数为( )
中,∠D=100°,∠DAB的平分线AE交DC于点E,连接BE,若AE=AB,则∠EBC的度数为( )
A.30°B.50°C.80°D.100°
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,菱形ABCD的周长为16 cm,∠BAD=120°对角线AC,BD相交于点O,过点O作BC的垂线交BC于点E,交AD于点F,求EF长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,正六边形ABCDEF在直角坐标系的位置如图所示,A(﹣2,0),点B在原点,把正六边形ABCDEF沿x轴正半轴作无滑动的连续翻转,每次翻转60°,经过5次翻转之后,点B的坐标是______.

-
科目: 来源: 题型:
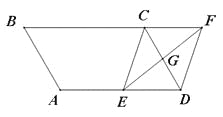
查看答案和解析>>【题目】(7分)如图,平行四边形ABCD中,AB=3cm,BC=5cm,∠B=60°,G是CD的中点,E是边AD上的动点,EG的延长线与BC的延长线交于点F,连接CE,DF.
(1)求证:四边形CEDF是平行四边形;
(2)①当AE= cm时,四边形CEDF是矩形;
②当AE= cm时,四边形CEDF是菱形;(直接写出答案,不需要说明理由)
相关试题

