【题目】如图,菱形ABCD的周长为16 cm,∠BAD=120°对角线AC,BD相交于点O,过点O作BC的垂线交BC于点E,交AD于点F,求EF长.

参考答案:
【答案】EF=![]() .
.
【解析】
根据菱形的性质得出AC、AO的长,在RT△AOB中求出OB,进而得到BD的长,利用菱形面积等于对角线乘积的一半,也等于BC×EF,则EF的长即可求出.
∵菱形ABCD的周长为16 cm,
∴AB=BC=CD=AD=4 cm,
∵∠BAD=120°,
∴∠BAC=![]() ∠BAD=
∠BAD=![]() ×120°=60°,
×120°=60°,
∴△ABC是等边三角形,
∴AC=AB=4 cm,
∴AO=![]() AC=2cm,
AC=2cm,
在Rt△AOB中,OB=![]() =
=![]() cm,
cm,
∴AB=2OB=![]() cm,
cm,
∵EF![]() BC,
BC,
∴S菱形ABCD=![]() AC
AC![]() BD=BC
BD=BC![]() EF,
EF,
∴EF=![]() .
.
-
科目: 来源: 题型:
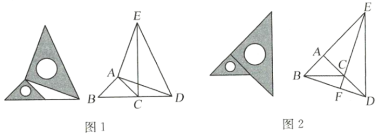
查看答案和解析>>【题目】把两个大小不同的等腰直角三角板按照一定的规则放置:“在同一平面内将直角顶点叠合”.
(1)图1是一种放置位置及由它抽象出的几何图形,
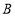 、
、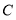 、
、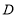 在同一条直线上,联结
在同一条直线上,联结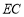 . 请找出图中的全等三角形(结论中不含未标识的字母),并说明理由;
. 请找出图中的全等三角形(结论中不含未标识的字母),并说明理由;(2)图2也是一种放置位置及由它抽象出的几何图形,
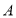 、
、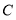 、
、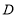 在同一条直线上,联结
在同一条直线上,联结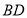 、
、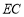 ,并延长
,并延长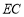 与
与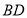 交于点
交于点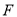 .请找出线段
.请找出线段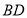 和
和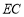 的位置关系,并说明理由;
的位置关系,并说明理由;(3)请你:
①画出一个符合放置规则且不同于图1和图2所放位置的几何图形;
②写出你所画几何图形中线段
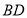 和
和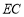 的位置和数量关系;
的位置和数量关系;③上面第②题中的结论在按照规则放置所抽象出的几何图形中都存在吗?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平行四边形
 中,∠D=100°,∠DAB的平分线AE交DC于点E,连接BE,若AE=AB,则∠EBC的度数为( )
中,∠D=100°,∠DAB的平分线AE交DC于点E,连接BE,若AE=AB,则∠EBC的度数为( )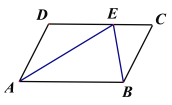
A.30°B.50°C.80°D.100°
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知关于x的一元二次方程x2+2x+
 =0有两个不相等的实数根,k为正整数.
=0有两个不相等的实数根,k为正整数.(1)求k的值;
(2)当此方程有一根为零时,直线y=x+2与关于x的二次函数y=x2+2x+
 的图象交于A、B两点,若M是线段AB上的一个动点,过点M作MN⊥x轴,交二次函数的图象于点N,求线段MN的最大值.
的图象交于A、B两点,若M是线段AB上的一个动点,过点M作MN⊥x轴,交二次函数的图象于点N,求线段MN的最大值. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,正六边形ABCDEF在直角坐标系的位置如图所示,A(﹣2,0),点B在原点,把正六边形ABCDEF沿x轴正半轴作无滑动的连续翻转,每次翻转60°,经过5次翻转之后,点B的坐标是______.

-
科目: 来源: 题型:
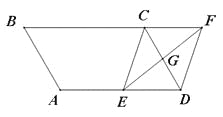
查看答案和解析>>【题目】(7分)如图,平行四边形ABCD中,AB=3cm,BC=5cm,∠B=60°,G是CD的中点,E是边AD上的动点,EG的延长线与BC的延长线交于点F,连接CE,DF.
(1)求证:四边形CEDF是平行四边形;
(2)①当AE= cm时,四边形CEDF是矩形;
②当AE= cm时,四边形CEDF是菱形;(直接写出答案,不需要说明理由)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD是正方形,点E是边BC的中点,∠AEF=90°,且EF交正方形外角平分线CF于点F.

(1)求证:AE=EF;
(2)如图2,若把条件“点E是边BC的中点”改为“点E是边BC上的任意一点”,其余条件不变,(1)中的结论是否仍然成立? ;(填“成立”或“不成立”);
(3)如图3,若把条件“点E是边BC的中点”改为“点E是边BC延长线上的一点”,其余条件仍不变,那么结论AE=EF是否成立呢?若成立请证明,若不成立说明理由.
相关试题

