搜索
【题目】阅读下面的材料：把形如
的二次三项式（或其中一部分）配成完全平方的形式，叫做配方法．配方的基本形式是完全平方公式的逆运用，即
．
例如：
________
________
________．
以上是
的三种不同形式的配方（即“余项”分别是常数、一次项、二次项–见横线上的部分）．根据阅读材料解决以下问题：
仿照上面的例子，写出
三种不同形式的配方；
将
配方（至少写出两种形式）；
已知
，求
、
、
的值．
参考答案：
【答案】(1) 见解析;(2)见解析;(3) a=2，b=4，c=3．
【解析】
（1）（2）运用配方法、阅读材料可得x2－4x＋2和a2＋ab＋b2的配方也可分为常数项、一次项、二次项三种不同形式；（3）运用配方法把原式化为平方和的形式，根据非负数的性质解答即可.
解：
的三种配方分别为：
，
，
；
；
∵
，
∴
，
，
，
∴
，
，
，
∴
，
，
．
-
科目： 来源： 题型：
查看答案和解析>>【题目】国庆假期期间，某单位8名领导和320名员工集体外出进行素质拓展活动，准备租用45座大车或30座小车．若租用2辆大车3辆小车共需租车费1700元；若租用3辆大车2辆小车共需租车费1800元
（1）求大、小车每辆的租车费各是多少元？
（2）若每辆车上至少要有一名领导，每个人均有座位，且总租车费用不超过3100元，求最省钱的租车方案．
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知，△ABC中，∠ACB＝90°，AC＝BC，点E是BC上一点，连接AE
（1）如图1，当AE平分∠BAC时，EH⊥AB于H，△EHB的周长为10m，求AB的长；
（2）如图2，延长BC至D，使DC＝BC，将线段AE绕点A顺时针旋转90°得线段AF，连接DF，过点B作BG⊥BC，交FC的延长线于点G，求证：BG＝BE．
-
科目： 来源： 题型：
查看答案和解析>>【题目】阅读材料，请回答下列问题
材料一：我国古代数学家秦九韶在《数书九章》中记述了“三斜求积术”，即已知三角形的三边长，求它的面积．用现代式子表示即为：S＝
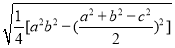…①（其中a，b，c为三角形的三边长，S为面积）而另一个文明古国古希腊也有求三角形面积的“海伦公式”；S＝
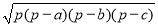……②（其中p＝
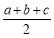）材料二：对于平方差公式：a2﹣b2＝（a+b）（a﹣b）
公式逆用可得：（a+b）（a﹣b）＝a2﹣b2，
例：a2﹣（b+c）2＝（a+b+c）（a﹣b﹣c）
（1）若已知三角形的三边长分别为3、4、5，请试分别运用公式①和公式②，计算该三角形的面积；
（2）你能否由公式①推导出公式②？请试试．
-
科目： 来源： 题型：
查看答案和解析>>【题目】商场某种商品平均每天可销售30件，每件盈利50元。为了尽快减少库存，商场决定采取适当的降价措施。经调查发现，每件商品每降价1元，商场平均每天可多售出2件。设每件商品降价
元。据此规律，请回答：（1）商场日销售量增加_____件，每件商品盈利_____元（用含
的代数式表示）。（2）在上述条件不变、销售正常情况下，每件商品降价多少元时，商场日盈利可达到2100元？
-
科目： 来源： 题型：
查看答案和解析>>【题目】关于x的一元二次方程（c+a）x2+2bx+(c-a)=0,其中a、b、c分别为△ABC三边的长．
（1）如果方程有两个相等的实数根，试判断△ABC的形状并说明理由；
（2）已知a:b:c=3:4:5,求该一元二次方程的根.
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在矩形ABCD中，对角线BD的垂直平分线MN与AD相交于点M，与BD相交于点O，与BC相交于点N，连接BM、DN．
求证：四边形BMDN是菱形；
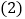若
，
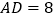，求菱形BMDN的面积和对角线MN的长．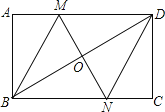
相关试题
