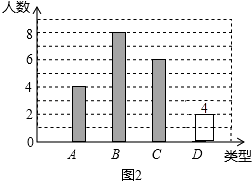
【题目】某校260名学生参加植树活动,要求每人植4﹣7棵,活动结束后随机抽查了20名学生每人的植树量,并分为四种类型,A:4棵;B:5棵;C:6棵;D:7棵,将各类的人数绘制成扇形图(如图1)和条形图(如图2). 
回答下列问题:
(1)补全条形图;
(2)写出这20名学生每人植树量的众数、中位数;
(3)请你计算平均数,并估计这260名学生共植树多少棵?
参考答案:
【答案】
(1)解:D类的人数是:20×10%=2(人).
(2)解:众数为5棵,中位数为5棵
(3)解: ![]() =
= ![]() =5.3(棵).
=5.3(棵).
估计260名学生共植树5.3×260=1378(棵)
【解析】(1)利用总人数20乘以对应的百分比即可求得D类的人数,从而补全直方图;(2)根据众数、中位数的定义即可直接求解;(3)首先求得调查的20人的平均数,乘以总人数260即可.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,CD⊥AB,EF⊥AB,垂足分别为D、F,∠1=∠2,
(1)试判断DG与BC的位置关系,并说明理由.
(2)若∠A=70°,∠BCG=40°,求∠AGD的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,在△ABC中,AB=AC,以AB为直径的⊙O交BC于点D,过点D作DE⊥AC于点E.

(1)请说明DE是⊙O的切线;
(2)若∠B=30°,AB=8,求DE的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】整式x2+kx+16为某完全平方式展开后的结果,则k的值为( )
A.4B.﹣4C.±4D.±8
-
科目: 来源: 题型:
查看答案和解析>>【题目】用10个球设计一个摸球游戏,使得:
(1)摸到红球的机会是
 .
.(2)摸到红球的机会是
 ,摸到黄球的机会是
,摸到黄球的机会是 .
.(3)你还能设计一个符合下列条件的游戏吗?为什么?
摸到红球的机会是
 ,摸到黄球的机会是
,摸到黄球的机会是 ,摸到绿球的机会是
,摸到绿球的机会是 .
. -
科目: 来源: 题型:
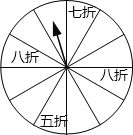
查看答案和解析>>【题目】如图,某酒店为了吸引顾客,设立了一个可以自由转动的装盘,并规定:顾客消费100元以上(不包括100元),就能获得一次转动转盘的机会,如果转盘停止后,若指针正好对准八折、七折、五折区域,顾客就可以获得此待遇(转盘分成12等份).
(1)甲顾客消费了90元,是否可获得转动转盘的机会?
(2)乙顾客消费120元,获得打折待遇的概率是多少?他获得八折、七折待遇的概率分别是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC 中,∠B 与∠C 的平分线交于点O, 过O 点作DE ∥BC,分别交AB、AC于D、E,若AB=5,AC=4,求△ADE 的周长.

相关试题

