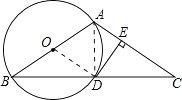
【题目】已知:如图,在△ABC中,AB=AC,以AB为直径的⊙O交BC于点D,过点D作DE⊥AC于点E. 
(1)请说明DE是⊙O的切线;
(2)若∠B=30°,AB=8,求DE的长.
参考答案:
【答案】
(1)解:连接OD,则OD=OB,
∴∠B=∠ODB.
∵AB=AC,
∴∠B=∠C.
∴∠ODB=∠C.
∴OD∥AC.(2分)
∴∠ODE=∠DEC=90°.
∴DE是⊙O的切线.
(2)解:连接AD,
∵AB是⊙O的直径,
∴∠ADB=90°.(1分)
∴ ![]() .(2分)
.(2分)
又∵AB=AC,
∴CD=BD= ![]() ,∠C=∠B=30°.(2分)
,∠C=∠B=30°.(2分)
∴ ![]() .(1分)
.(1分)
【解析】(1)要想证DE是⊙O的切线,只要连接OD,求证∠ODE=90°即可.(2)利用直角三角形和等边三角形的特点来求DE的长.
【考点精析】本题主要考查了切线的判定定理和解直角三角形的相关知识点,需要掌握切线的判定方法:经过半径外端并且垂直于这条半径的直线是圆的切线;解直角三角形的依据:①边的关系a2+b2=c2;②角的关系:A+B=90°;③边角关系:三角函数的定义.(注意:尽量避免使用中间数据和除法)才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在△ABC中,AB=AC,BD⊥AC于D,CE⊥AB于E,BD,CE相交于F.
求证:AF平分∠BAC.

-
科目: 来源: 题型:
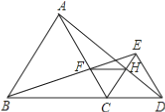
查看答案和解析>>【题目】如图,已知点B、C、D在同一条直线上,△ABC和△CDE都是等边三角形.BE交AC于F,AD交CE于H,求证:
(1)△BCE≌△ACD;
(2)CF=CH;
(3)△FCH是等边三角形;
(4)FH∥BD.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,CD⊥AB,EF⊥AB,垂足分别为D、F,∠1=∠2,
(1)试判断DG与BC的位置关系,并说明理由.
(2)若∠A=70°,∠BCG=40°,求∠AGD的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】整式x2+kx+16为某完全平方式展开后的结果,则k的值为( )
A.4B.﹣4C.±4D.±8
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校260名学生参加植树活动,要求每人植4﹣7棵,活动结束后随机抽查了20名学生每人的植树量,并分为四种类型,A:4棵;B:5棵;C:6棵;D:7棵,将各类的人数绘制成扇形图(如图1)和条形图(如图2).

回答下列问题:
(1)补全条形图;
(2)写出这20名学生每人植树量的众数、中位数;
(3)请你计算平均数,并估计这260名学生共植树多少棵? -
科目: 来源: 题型:
查看答案和解析>>【题目】用10个球设计一个摸球游戏,使得:
(1)摸到红球的机会是
 .
.(2)摸到红球的机会是
 ,摸到黄球的机会是
,摸到黄球的机会是 .
.(3)你还能设计一个符合下列条件的游戏吗?为什么?
摸到红球的机会是
 ,摸到黄球的机会是
,摸到黄球的机会是 ,摸到绿球的机会是
,摸到绿球的机会是 .
.
相关试题

