【题目】低碳生活备受关注.小明为了了解人们到某超市购物时使用购物袋的情况,利用星期日到该超市对部分购物者进行调查,并把调查结果绘制成两幅不完整的统计图.假设当天每人每次购物时都只用一个环保购物袋(可降解)或塑料购物袋(不可降解).

根据以上信息,回答下列问题:
(1)小明这次调查到的购物人数是 人次;
(2)补全两幅统计图;
(3)若当天到该超市购物者共有2000人次,请你估计使用塑料购物袋有 人次;环保购物袋有 人次;扇形C的圆心角是 度
参考答案:
【答案】(1)120;(2)补图见解析;(3)1200,800,36°.
【解析】试题分析:(1)由C的人数除以所占的百分比即可确定出调查的购物人数;
(2)由总人数减去A,C,D的人数求出B的人数,补全条形统计图;求出A与D所占的百分比,补全扇形统计图即可;
(3)求出A与C百分比之和,以及B与D百分比之和,分别乘以2000即可得到结果.
试题解析:解:(1)根据题意得:12÷10%=120(人次),则小明这次调查到的购物人数是120人次;
(2)B的人数为120﹣(36+12+42)=30(人次),A的百分比为![]() ×100%=30%;D的百分比为
×100%=30%;D的百分比为![]() ×100%=35%,补全统计图,如图所示:
×100%=35%,补全统计图,如图所示:

(3)根据题意得:2000×(25%+35%)=1200(人次),2000×(30%+10%)=800(人次);则估计该天使用使用塑料购物袋有1200人次,环保购物袋有800人次.扇形C的圆心角=360°×10%=36°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】合并下列多项式中的同类项:
(1)3x2+4x﹣2x2﹣x+x2﹣3x﹣1;
(2)﹣a2b+2a2b;
(3)a3﹣a2b+ab2+a2b﹣2ab2+b3;
(4)2a2b+3a2b﹣
 a2b
a2b -
科目: 来源: 题型:
查看答案和解析>>【题目】(1)﹣
 a2bc+
a2bc+ cba2
cba2(2)7ab﹣3a2b2+7+8ab2+3a2b2﹣3﹣7ab
(3)(﹣x+2x2+5)+(4x2﹣3﹣6x)
(4)(2x2﹣
 +3x)﹣4(x﹣x2+
+3x)﹣4(x﹣x2+ )
) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,ABCD中,BD⊥AD,∠A=45°,E、F分别是AB,CD上的点,且BE=DF,连接EF交BD于O.
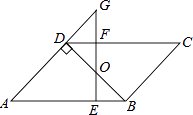
(1)求证:BO=DO;
(2)若EF⊥AB,延长EF交AD的延长线于G,当FG=1时,求AD的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】为倡导低碳生活,绿色出行,某自行车俱乐部利用周末组织“远游骑行”活动.自行车队从甲地出发,途径乙地短暂休息完成补给后,继续骑行至目的地丙地,自行车队出发1小时后,恰有一辆邮政车从甲地出发,沿自行车队行进路线前往丙地,在丙地完成2小时装卸工作后按原路返回甲地,自行车队与邮政车行驶速度均保持不变,并且邮政车行驶速度是自行车队行驶速度的2.5倍,如图表示自行车队、邮政车离甲地的路程y(km)与自行车队离开甲地时间x(h)的函数关系图象,请根据图象提供的信息解答下列各题:

(1)自行车队行驶的速度是km/h;
(2)邮政车出发多少小时与自行车队首次相遇?
(3)邮政车在返程途中与自行车队再次相遇时的地点距离甲地多远? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直角梯形ABCD中,AB∥CD,∠DAB=90°,且∠ABC=60°,AB=BC,△ACD的外接圆⊙O交BC于E点,连接DE并延长,交AC于P点,交AB延长线于F.

(1)求证:CF=DB;
(2)当AD= 时,试求E点到CF的距离.
时,试求E点到CF的距离. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知OE是∠AOC的角平分线,OD是∠BOC的角平分线.
(1)若∠AOC=120°,∠BOC=30°,求∠DOE的度数;
(2)若∠AOB=90°,∠BOC=α,求∠DOE的度数.

相关试题

