【题目】如图是某种产品展开图,高为3cm.
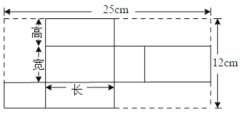
(1)求这个产品的体积.
(2)请为厂家设计一种包装纸箱,使每箱能装5件这种产品,要求没有空隙且要使该纸箱所用材料尽可能少(纸的厚度不计,纸箱的表面积尽可能小),求此长方体的表面积.
参考答案:
【答案】(1)长方形的体积为144cm3;(2)纸箱的表面积为516cm2.
【解析】
(1)根据已知图形得出长方体的高进而得出答案;
(2)设计的包装纸箱为15×6×8规格.
(1)长方体的高为3cm,则长方形的宽为(12-2×3)cm,长为![]() (25-3-6)cm,根据题意可得:
(25-3-6)cm,根据题意可得:
长方形的体积为:8×6×3=144(cm3);
(2)因为长方体的高为3cm,宽为6cm,长为8cm,
所以装5件这种产品,应该尽量使得6×8的面重叠在一起,纸箱所用材料就尽可能少,
这样的话,5件这种产品可以用15×6×8的包装纸箱,再考虑15×8的面积最大,所以15×8的面重叠在一起,纸箱所用材料就尽可能少,
所以设计的包装纸箱为15×6×8规格,该产品的侧面积分别为:
8×6=48(cm2),8×15=120(cm2),6×15=90(cm2)
纸箱的表面积为:2(120+48+90)=516(cm2).
-
科目: 来源: 题型:
查看答案和解析>>【题目】在一快递仓库里堆放着若干个相同的正方体快递件,管理员从正面看和从左面看这堆快递如图所示,则这正方体快递件最多有_____件.
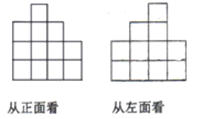
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,点O为坐标原点,正方形OABC的边OA、OC分别在x轴、y轴上,点B的坐标为(2,2),反比例函数
 (x>0,k≠0)的图像经过线段BC的中点D.
(x>0,k≠0)的图像经过线段BC的中点D.
(1)求k的值;
(2)若点P(x,y)在该反比例函数的图像上运动(不与点D重合),过点P作PR⊥y轴于点R,作PQ⊥BC所在直线于点Q,记四边形CQPR的面积为S,求S关于x的解析式并写出x的取值范围。
-
科目: 来源: 题型:
查看答案和解析>>【题目】有一个数值转换机,原理如图所示,若开始输入的x的值是7,可发现第1次输出的结果是12,第2次输出的结果是6,...依次继续下去

(1)请列式计算第3次到第8次的输出结果;
(2)你根据(1)中所得的结果找到了规律吗?计算2013次输出的结果是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】将正方形 ABCD (如图 1)作如下划分:
第1次划分:分别连接正方形ABCD对边的中点(如图2),得线段HF和EG,它们交于点M,此时图2中共有5个正方形;
第2次划分:将图2 左上角正方形AEMH再作划分,得图3,则图3 中共有9个正方形;
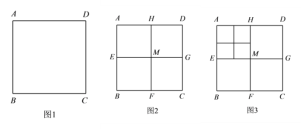
(1)若每次都把左上角的正方形依次划分下去,则第100次划分后,图中共有 个正方形;
(2)继续划分下去,第几次划分后能有805个正方形?写出计算过程.
(3)按这种方法能否将正方形ABCD划分成有2015个正方形的图形?如果能,请算出是第几次划分,如果不能,需说明理由.
(4)如果设原正方形的边长为1,通过不断地分割该面积为1的正方形,并把数量关系和几何图形巧妙地结合起来,可以很容易得到一些计算结果,试着探究求出下面表达式的结果吧.
计算
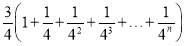 .( 直接写出答案即可)
.( 直接写出答案即可) -
科目: 来源: 题型:
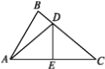
查看答案和解析>>【题目】如图,已知∠BAC=60° ,∠B=80° ,DE垂直平分AC交BC于点D,交AC于点E.
(1)求∠BAD的度数;
(2)若AB=10,BC=12,求△ABD的周长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中, AB=AC,点D为BC中点,点E在AB边上,连接DE,过点D作DE的垂线,交AC于点F.下列结论:①△BDE≌△ADF;②AE=CF;③BE+CF=EF;④S四边形AEDF=
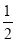 AD2,其中正确的结论是__________(填序号).
AD2,其中正确的结论是__________(填序号).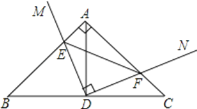
相关试题

